分数とは、ある数を 0 でない他の数で割った商を、横線の上(分子)に割られる数、横線の下(分母)に割る数を記して表したものです。 このページでは、分数の計算のやり方をまとめています。各項目では、加減乗除の四則計算について、それぞれの計算方法と簡単な計算例をご紹介してい 分数式とは まずはじめに、分数式とは 分母、分子に文字が入っている分数 のことだと思えばよいです。分数式は基本的に普通の分数と同じで 一番簡単な形になるまで変形しなくてはいけません 。 ここではその分数式を計算する方針と方法を説明します。途中に計算式が出てきますが、ここで理解する必要はありません。分数の計算の説明ページで計算方法は細かく説明していますので、ここでは名前だけ覚えてください。 分数の名称 分数は分母と分子にわかれます。 $\displaystyle\frac{分子(ぶんし)}{分母(ぶんぼ)}$ 分子と分母の間にある線の
分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料
分母が分数の計算
分母が分数の計算- 分数の計算方法を一覧にまとめました。 計算のやり方を忘れてしまったときには、こちらで確認しましょう。 分数の計算のやり方 分数の足し算のやり方 ①分母をそろえる ②分子どうしを足す ③約分する 〈分母が同じ分数の足し算〉 〈分母が違う分数の足し算〉 分数の引き算のやり方 ①正弦定理を利用して問題を解くときには,次のような分数型の方程式がしばしば登場しますここでは,正弦定理を利用するための準備として,分数型の方程式の変形を練習します (a) のように未知数が左辺の分子にある場合 両辺の分母にある を2つとも
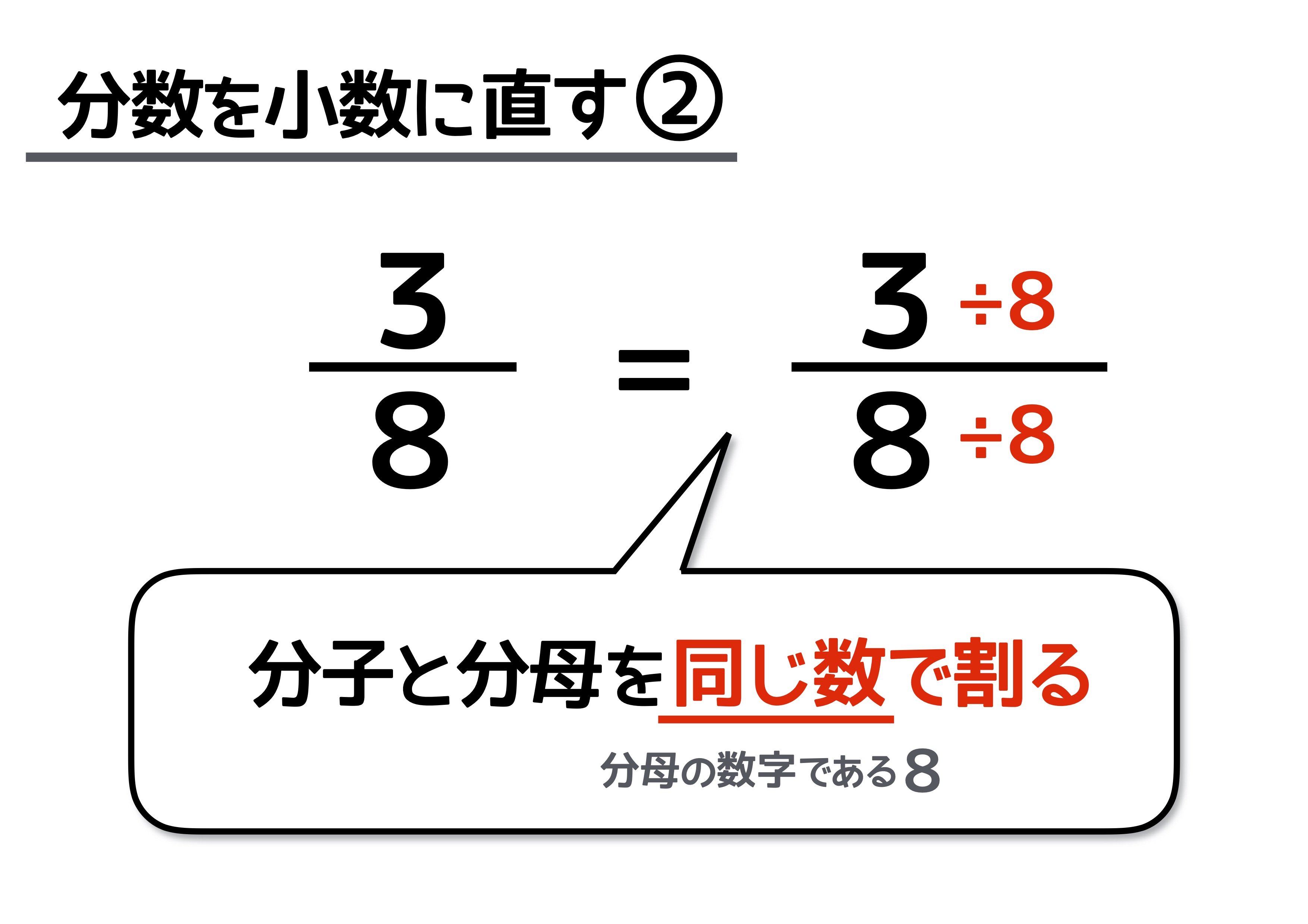



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ
理科の濃度計算などでよく出てくる方程式ですね。 今回の記事はこちらの動画でも解説しています(^^) Contents 分母にxの解き方! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか? 分母にxの解き方! 分数の方程式は、とにかく分母の有理化が必要な理由としては、通分することで分数同士を計算できるようにする必要があるからです。分母の有理化をしないと、計算できないのです。 練習問題:分母の有理化の計算 Q1 分母の有理化をしましょう $\displaystyle\frac{4}{\sqrt{8}}$分母が同じなら、分子だけを足し算・引き算すれば良いのが分数の計算。 では、分母が違う分数の計算はどうしたらよいでしょうか。 「通分」するんですね。覚えていましたか? 最低限覚えること 分母が違う足し算と引き算は、通分して分母をそろえてから計算します。 通分とはある数を
演習問題で理解を深める! 分数分の分数のやり方 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる!分母が同じ分数どうしのたし算・ひき算の学習プリントです。 約分などはありません。 分数のたし算・ひき算を初めて学習するタイミングなので、計算問題だけでなくテープ図による導入問題もつけてあります。 分子どうしを計算するだけなので計算手順はとても簡単ですが、なるべく分数の分母に分数を含む式 ここでは、分母に分数を含む式の計算のしかたについてみていきましょう。 次の式を簡単にしなさい 難しい分数式を考える前に、簡単な分数を例に考えてみましょう。 この分数式について考えてみます。
異分母分数の加法、減法の計算ができ、それを用いることができる。数量や図形について の技能 通分や約分という観点から分数の大きさについての豊かな感覚をもっているとともに、異分 母分数の加法、減法の意味や計算の仕方を理解することができる。数量や図形についての 知識 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。 分数の計算 まとめ こちらの記事では、 円で分数をあらわして、分母の違う分数をたしたりひいたりする"通分(つうぶん)"の解き方 を説明してきました。 はじめにお伝えした通り、 どん



1




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun
分数式の約分 分数 (式)には,分母と分子に同じ数 (式)を掛けたり,同じ数 (式)で割ったりしても値が変わらないという性質 A B = A × C B × C A B = A ÷ C B ÷ C があって,この性質を用いて約分することができます。 例題1 分数式 x2 3x 2 x2 − 2x − 3 を約分し分数のわり算を扱うときには「包含除」で考えることが理解するうえでの近道となります。分数のわり算は、以下のように計算しますね。 4 ÷ 2 5 分数のたし算異分母の計算 19年11月5日 通分大きさ比べ 19年11月5日 整数約数の求め方 19年11月5日 分数のひき算同分母の計算 19年11月5日 通分通分の仕方 19年11月5日 多言語算数練習問題PDF 日本語版|韓国・朝鮮語版|中国語版|ポルトガル語




え 幼稚園年長児にイキナリ 異分母の分数計算ですか はい 出来ます 七田式天六教室 本町教室及び魔法の折り紙オンライン教室は算数 数学のスペシャリストを育てます
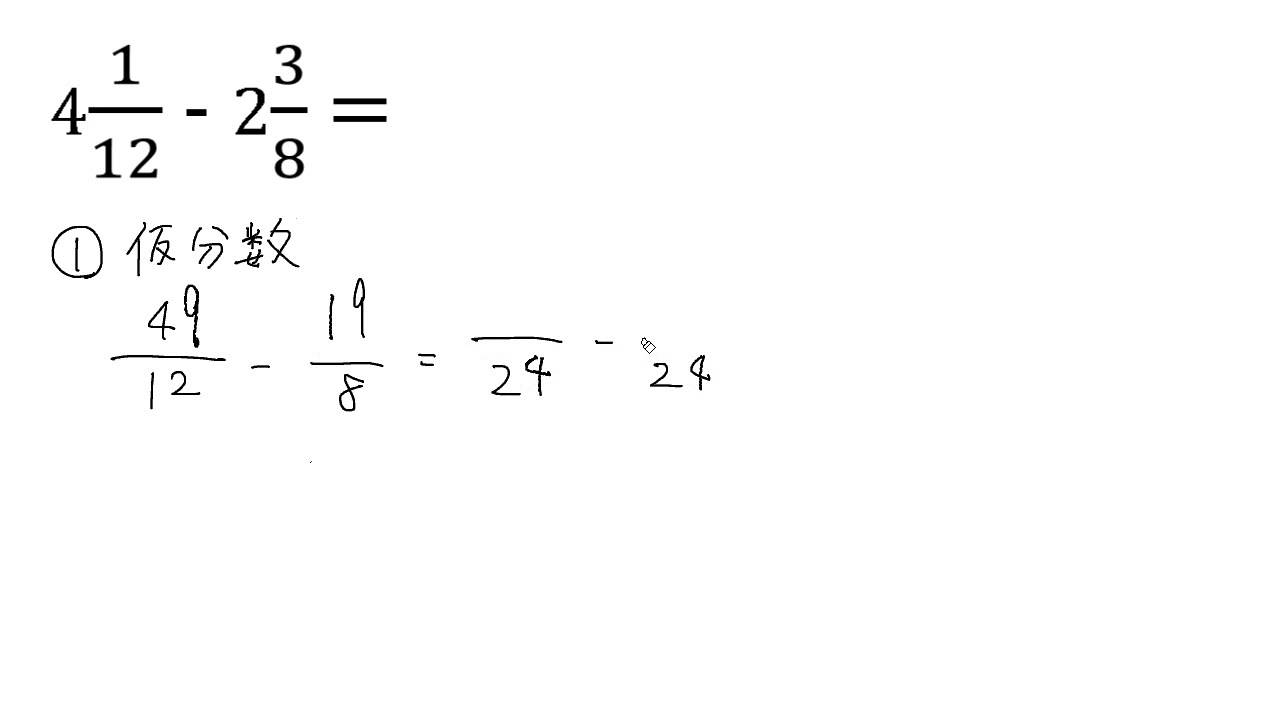



帯分数の引き算 通分あり Youtube
分数の計算のくふう 基本2 ここでは,分子が1の分数どうしの引き算を学習します。 1 1 例題5: - 4 5 ふつうは,次のように通分して求めます。 1 1 - 4 5 5 4 = - 1 = では,次の計算はどうでしょう。 1 1 例題6: - 19分数(有理数)の指数が付いている式は累乗根で表される式と同じものです.多くの場合,分数の指数を使って計算する方が累乗根のまま計算するよりも簡単になります. 分数(有理数)の指数の定義 a>0 であって m, n が正の整数であるとき a mnn = n√ 分数を分数で割るということ 例えば、2/5 ÷ 1/3 という計算をするとします。 2/5 ÷ 1/3 ですので、割る数の1/3が下へ落ちます。 つまり、1/3が分母にいき、2/5は分子です。




分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun




異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料
もっと詳しく: 約分のやり方と計算ツール (4) 1 4 と 2 3 を通分せよ。 (4) 1 4 の分母と分子に 3 をかけると 3 12 となります。 2 3 の分母と分子に 4 をかけると 8 12 となります。 分数の通分|苦手な人向け計算テクニックを丁寧解説 分母の違う分数をたしたりひいたりするときに必要な作業"通分(つうぶん)"。 "分数の通分" は、文部科学省の新学習指導要領でも、 小学校5年生で勉強 する算数の単元です。 この通分は、中7、繁分数の計算は、分母や分子にある分数の計算を先にする。 繁分数とは、分数の分母や分子がさらに分数になっているものをいいます。 8、次の分数の計算をしてみましょう。 ① , ② いかがでしょうか。だんだんとややこしくなってきましたが、要は上の1~7までの積み上げです。(電験3
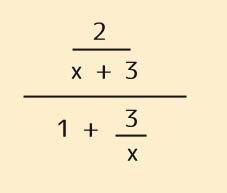



英語で分数の読み方と表現 何分の1 はどう言う 分子 分母は 話す英語 暮らす英語



3
分数計算の加算・減算・乗算・除算を思い出しましょう。 2つ以上の分数の分母を同じにそろえることを 通分するといい、 そろえた分母を共通な分母といいます 2 + 1 → 4 + 3 3 2 6 6 9 逆数 分子と分母を入れかえた数 1 → 2 2 1 10 足し算 同分母にして、分子だけを加えます 4分母に分数を含む分数式 分母に分数がある場合の分数式の計算方法をみてみましょう。 ① こんな場合です。うーん、どうやってとけばいいでしょうか。 そもそも分数とは でしたね。①の式を 割り算の形に変形してみましょう。ただ解く順番は整数でも分数でも同じなので難しいものではありません。 ここでは分数の四則演算のおさらいも含めて解説していきます。 分数の足し算・引き算 分数の足し算・引き算は、分母が同じ分数同士の場合には分子同士で計算をおこないます。




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo
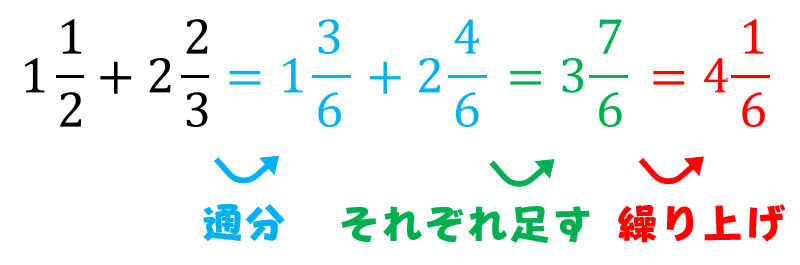



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun
学習する学年:小学生 1.分数のわりざんの説明 分数のわりざんは、分数のたしざんやひきざんを計算する時のように分母の数を揃える為に通分する必要がありませんので、とても簡単に計算して答えを出すことができます。 分数の計算という言葉を聞くと難しい印象を持つかと思いますが例 6 56 (部分分数の積分の計算例) Type 1 Type 2 Type 3 Type 4 Type 5 Type 6 これ を計算する. 分子の次数が分母の次数以上であるから, 分子を分母で割り のように変形する. 多項式部分は積分される. 残るは有理式の積分である. これを計算すると となる. よって を得る. 例 6 61 (有理同じ分母の分数のたし算、ひき算を練習できます (プリント4枚) 小学4年生 分数 練習問題プリント 小学4年生の算数 分数の大きさ(1) 真分数・仮分数・帯分数の意味 練習問題プリント 小学4年生の算数・分数の大きさ真分数・仮分数・帯分数の意味問題プリントを無料




分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
ツイート 無料ダウンロード・印刷できる小学5年生の算数プリント。 分母のちがう分数を、通分、約分して引き算する練習問題です。 異分母の分数の引き算(1) 答え 異分母の分数の引き算(2) 答え 異分母の分数の引き算(3) 答え分母に分数を含む分数式の計算方法を知りたい 次の式の計算をせよ。 「この計算方法を教えて下さい。 」という質問をいただきました。 では、実際に計算していってみましょう! ! まず、分母の を計算してみましょう。 となります。 となります。無学年で分数に関する演習をする計算プリントです。 進級テストつき! 分数計算トレーニング (無学年) ・仮分数⇔帯分数 ・等しい分数 ・倍数/公倍数 ・約数/公約数 ・約分/通分 ・同分母たし算/引き算 ・分数のたし算/引き算 ・分数のかけ算 ・分数のわり算 ・10回のテスト形式で計算力を
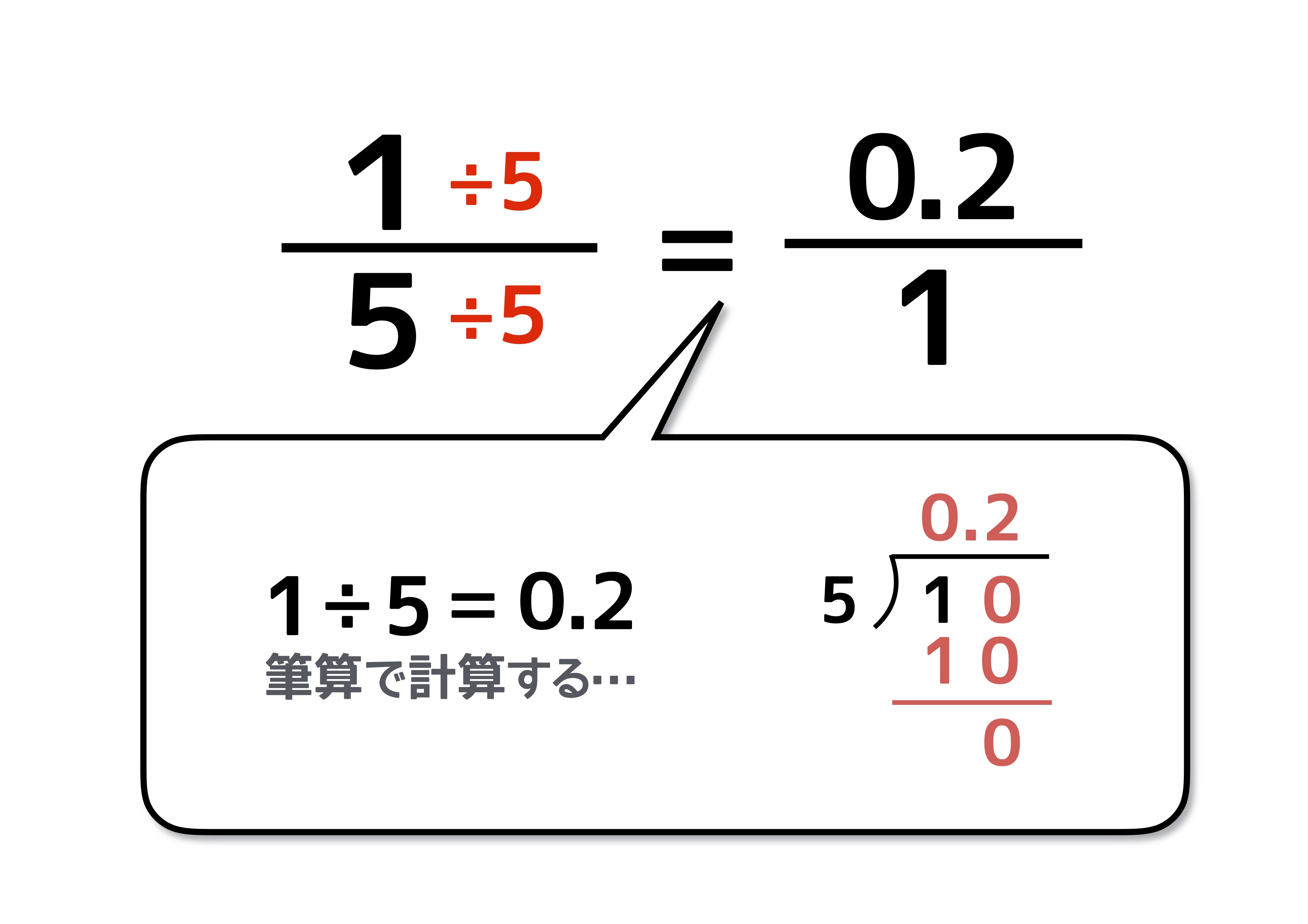



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ
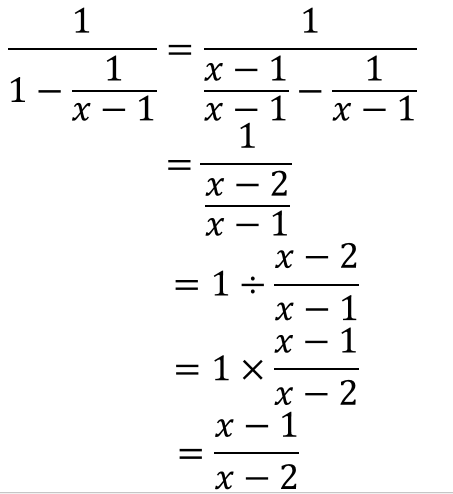



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
分数の計算を行っていて 分母や分子にさらに分数がある場合の 計算方法について お話をしていきます。 例えば この様な計算です。 一瞬 「あれ?」 と思うかもしれませんが、 分数の計算のルールにしたがって 落ち着いて計算を行えば、 ちゃんと答えを求めることができます。 それでは
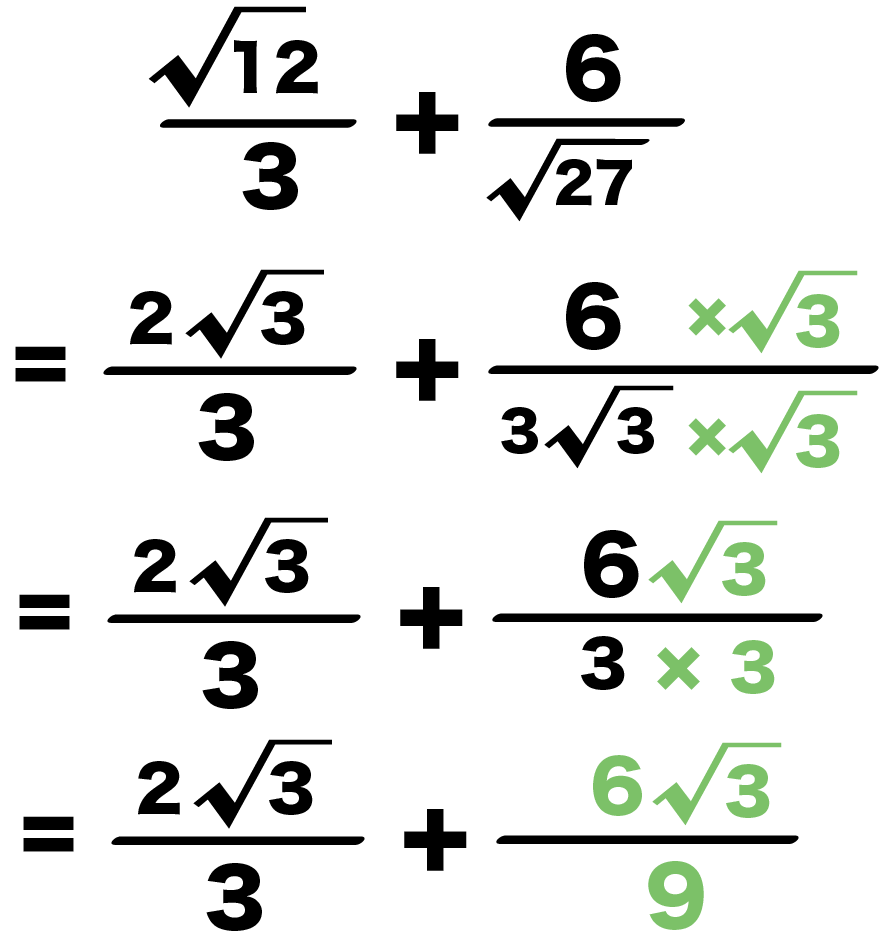



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




割り算をしたとき その数は分母と分子のどっちに行くか覚えよう 中学や高校の数学の計算問題




帯分数の足し算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス




分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




文字の入った分数の約分とマイナスの扱い 分数の文字式の計算 Youtube
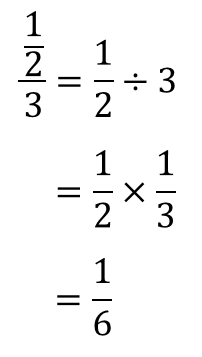



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
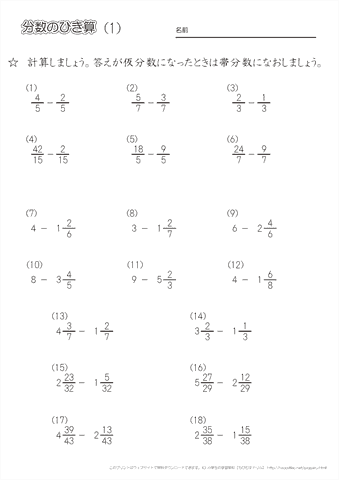



小学4年生の算数 同じ分母の分数のひき算 練習問題プリント ちびむすドリル 小学生




分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun
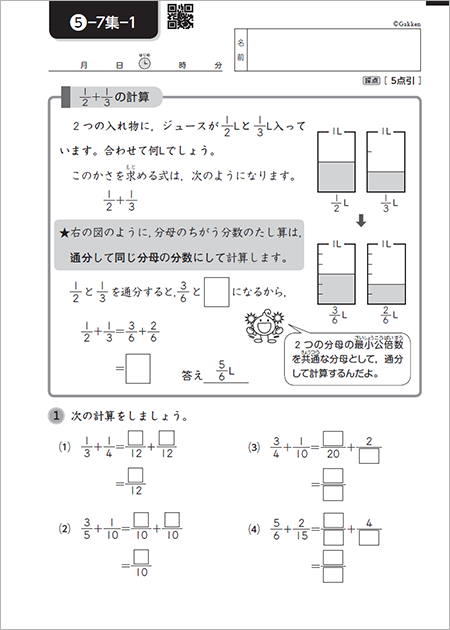



学研教室




分数の引き算の計算プリント 分母が異なる問題 全240問無料 算数パラダイス




数学 文字のある分数 分数の計算 高校数学tv Youtube




数学 分数の中に分数がある場合の計算の方法




小学算数 にがてな分数の計算に強くなる Amazon Com Books




分数の足し算の計算プリント 分母が異なる問題 全240問無料 算数パラダイス
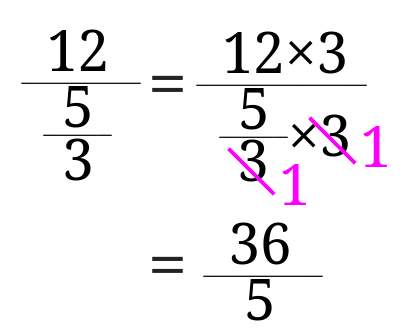



分数の中に分数のような繁分数の計算の仕方がわからない さびねこ中学校
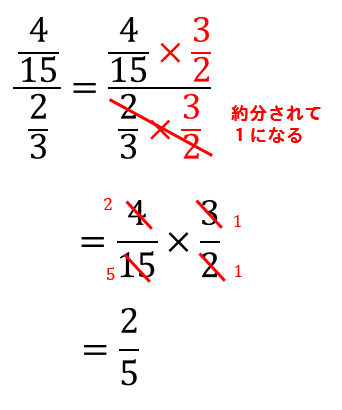



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
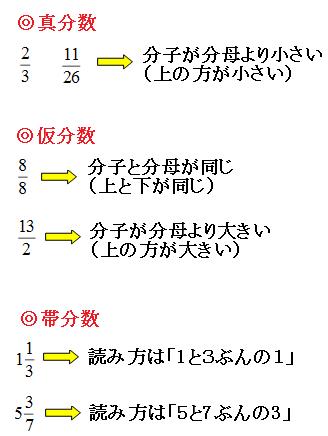



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利
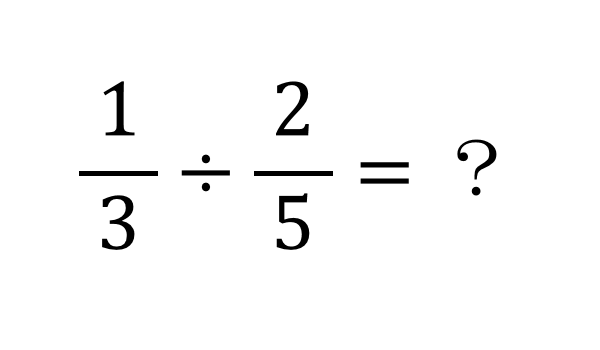



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ
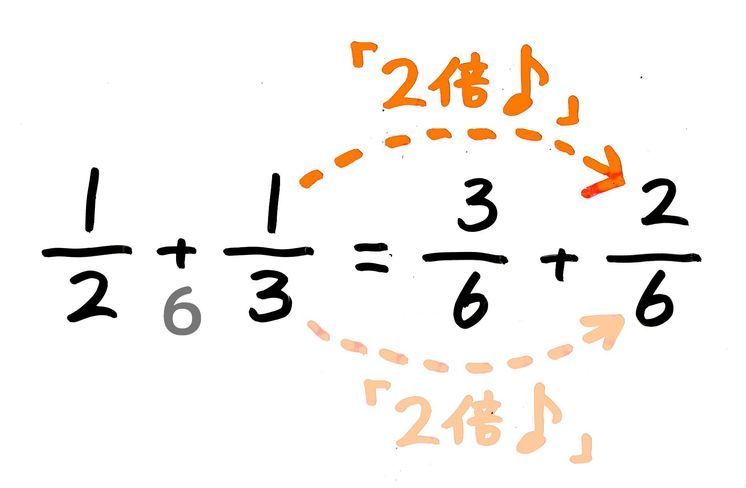



小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館



1
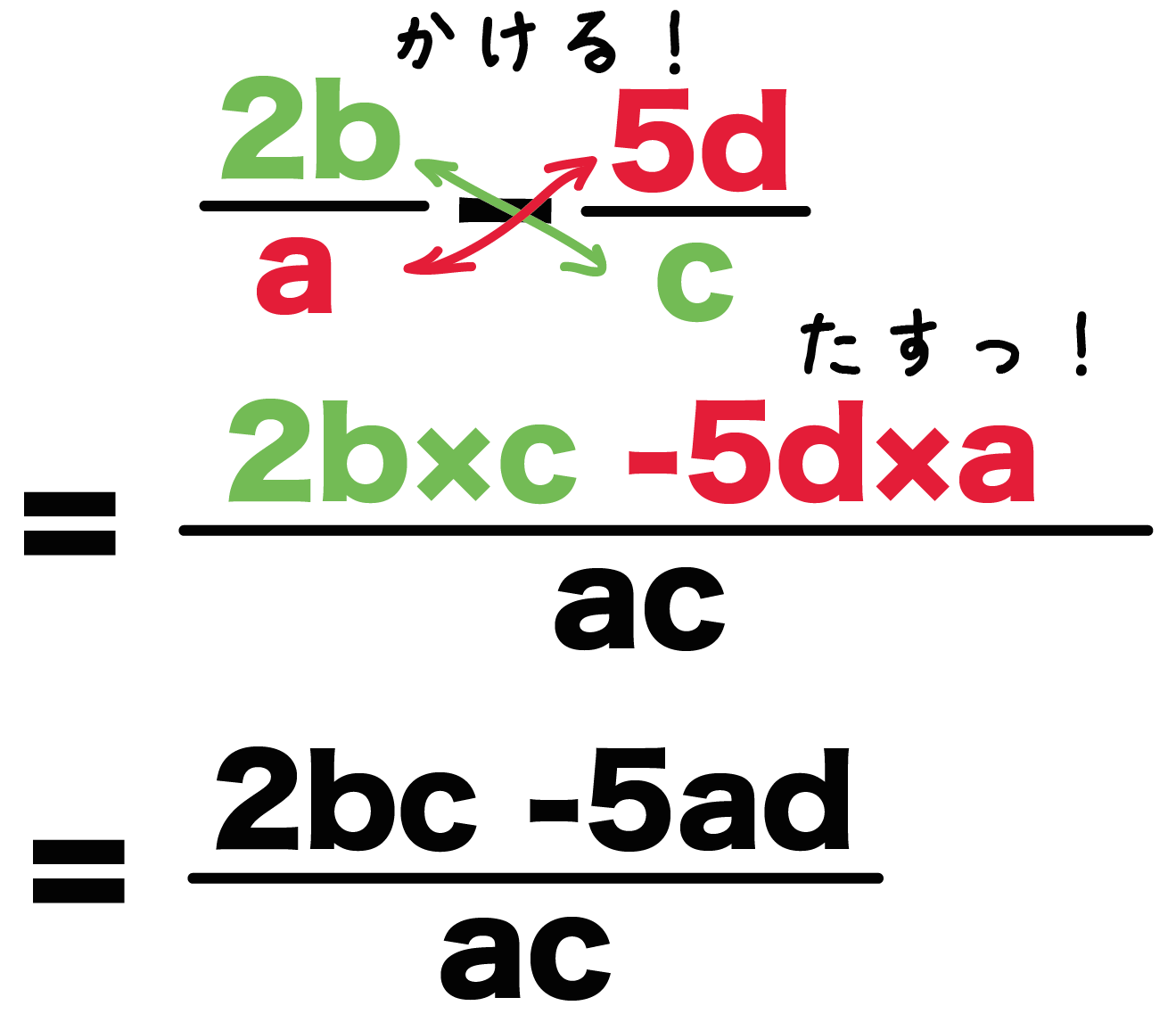



3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題
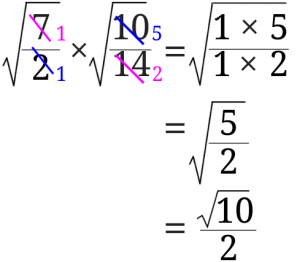



ルートの中が分数の時の掛け算の計算の仕方のコツって さびねこ中学校



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料
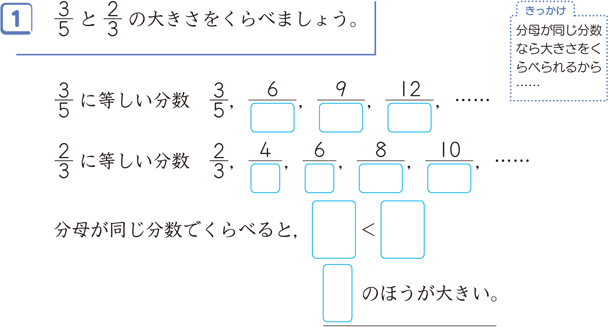



通分と約分 算数用語集




文字式の分数の問題です 文字式の計算では分母をはらわず 通分することと Okwave
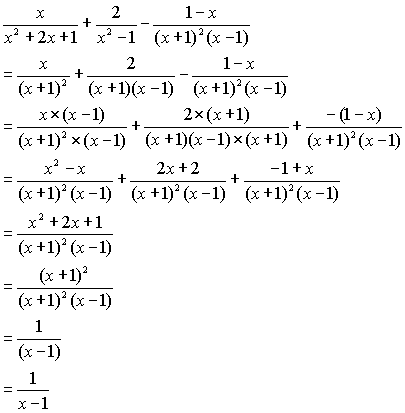



分数の復習と分数式の計算
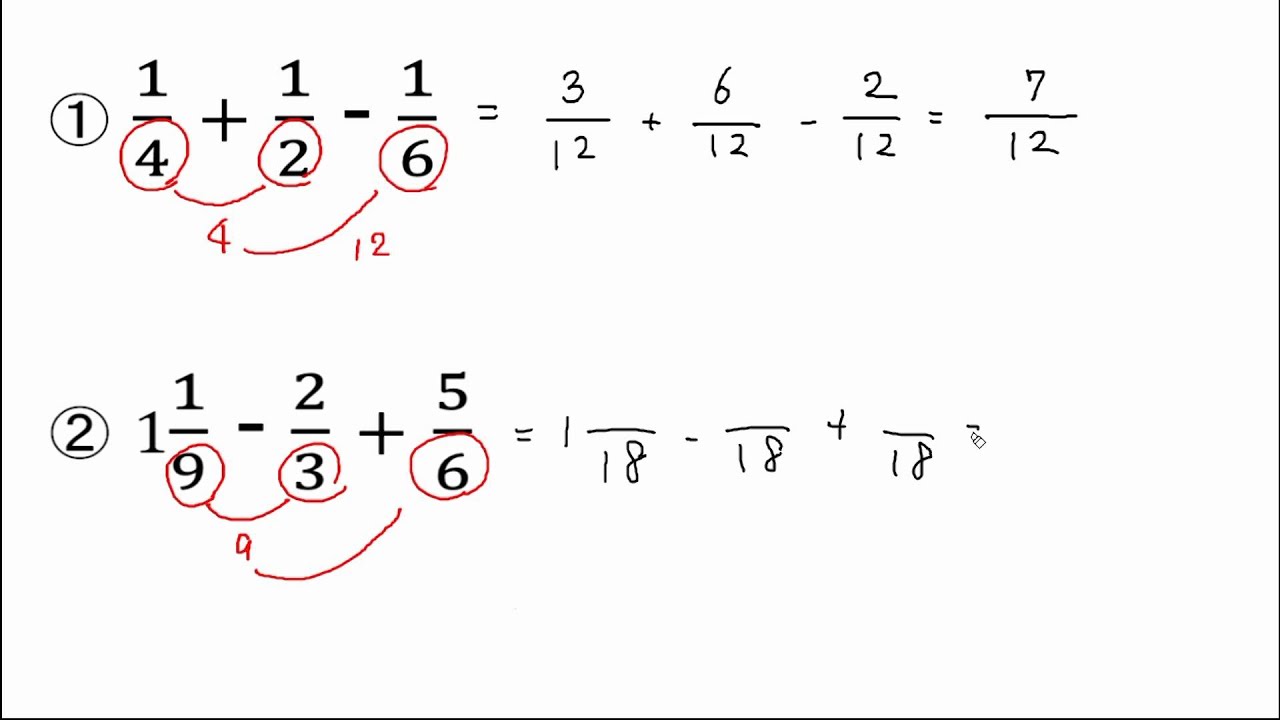



足し算とひき算が混じった分数の計算 Youtube




分数の足し算 分母が異なる 計算ドリル 問題集 数学fun




分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分母にxのある方程式の解き方を教えて頂けますか 分母にxのある方程 数学 教えて Goo
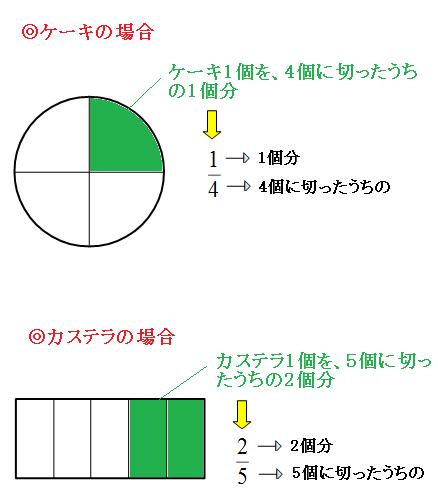



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




単項式の乗除 分数の割り算の問題は 分子と分母の分け方に注目 中学や高校の数学の計算問題



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料




分数の計算 X 100 5 恥ずかしながら分数の計算を忘れてしまい 数学 教えて Goo
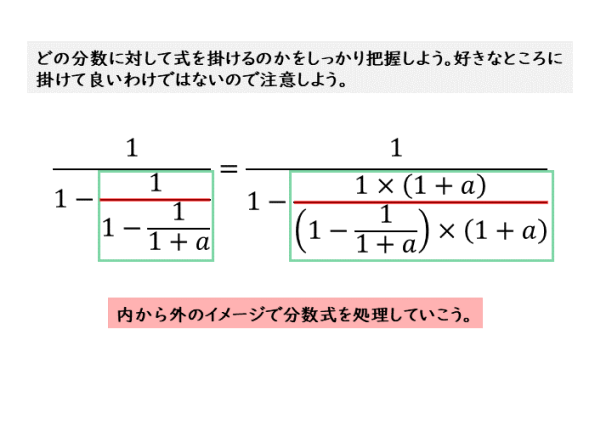



式と証明 繁分数式の計算について 日々是鍛錬 ひびこれたんれん




Logの足し算は掛け算で計算するのじゃないんですか なぜここは通分なんですか Clear
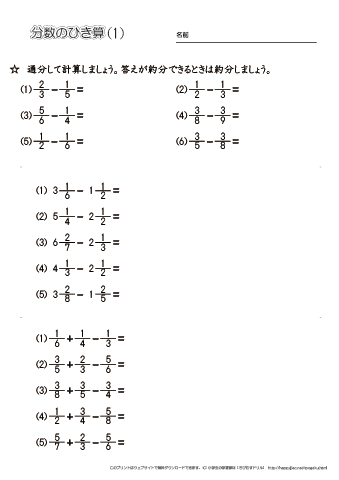



小学5年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生



秋篠理数 算数教室の さあさあ お勉強だよ




数学 分数の中に分数がある場合の計算の方法
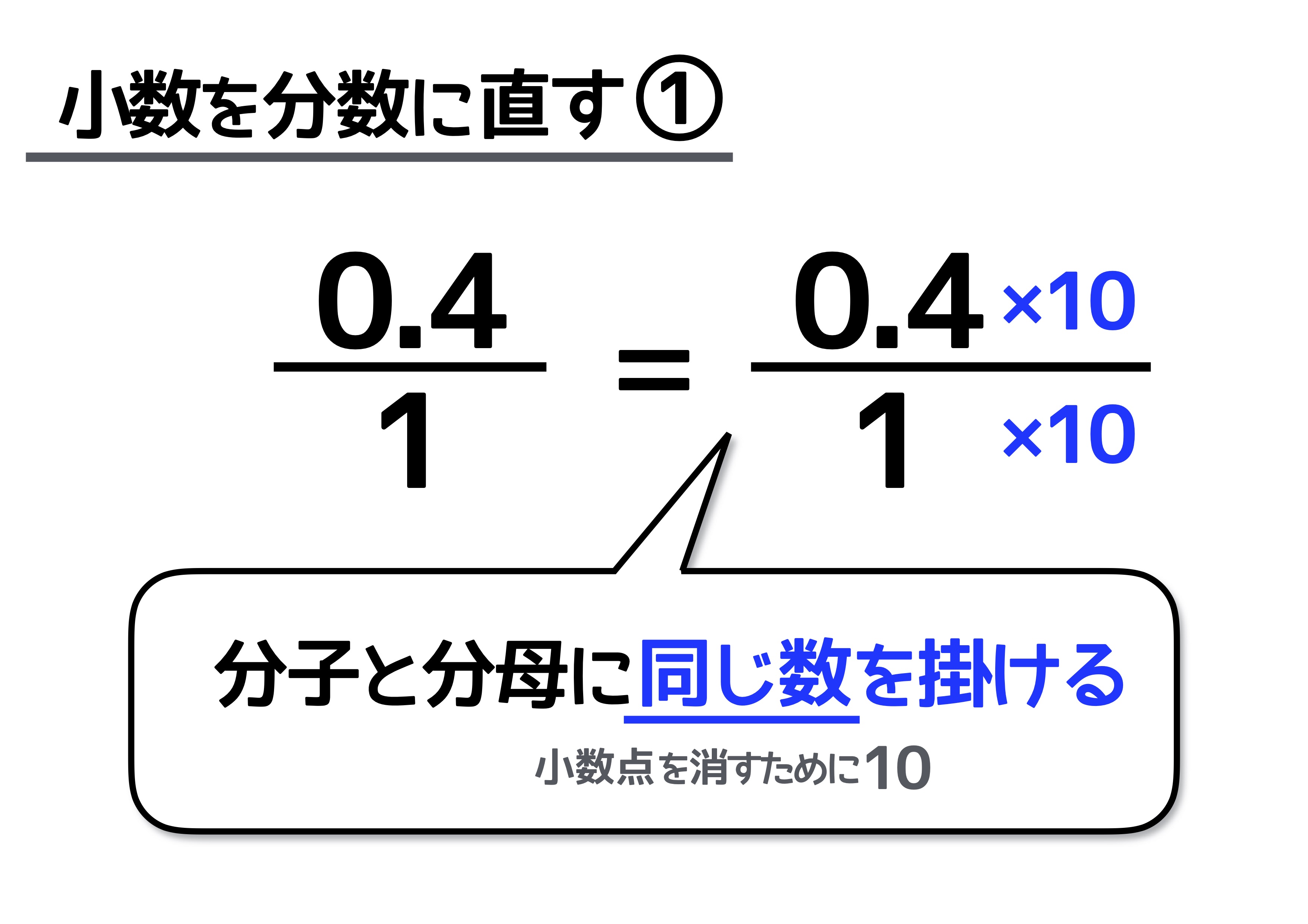



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ
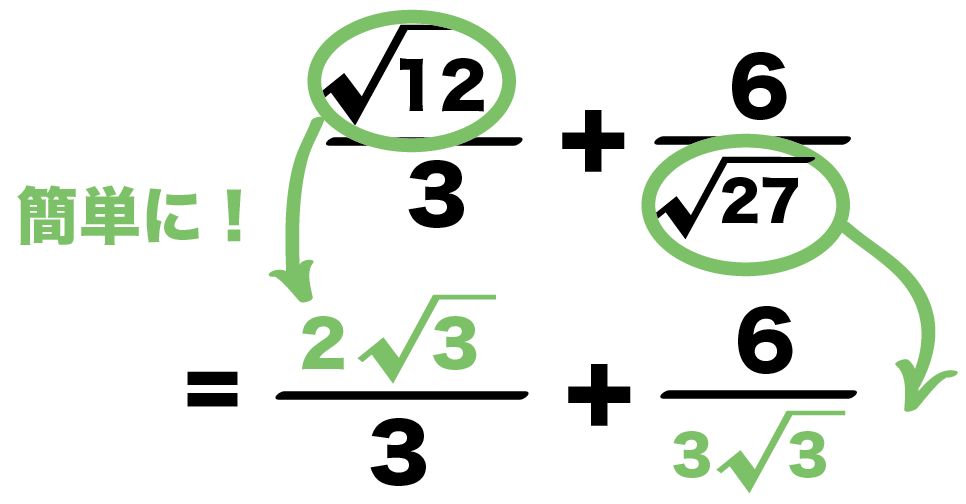



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




小学5年生 算数 無料問題集 分母が違う分数の引き算 おかわりドリル
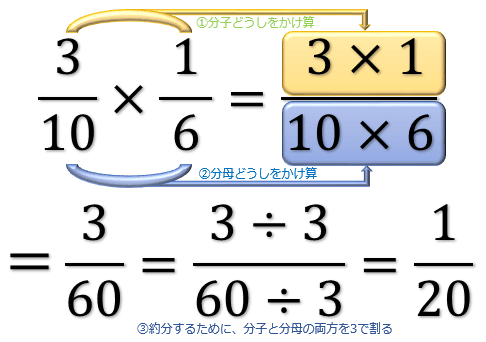



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分母が違う分数の足し算 通分して計算する理由は分配法則を考えればわかる 数学の面白いこと 役に立つことをまとめたサイト



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料
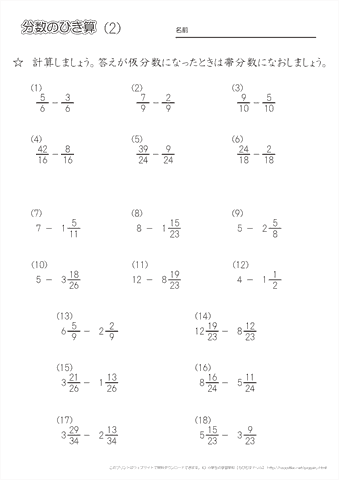



小学4年生の算数 同じ分母の分数のひき算 練習問題プリント ちびむすドリル 小学生




数学 分数の中に分数がある場合の計算の方法



3




小学3年生 算数 無料問題集 分母が同じ分数の引き算 おかわりドリル
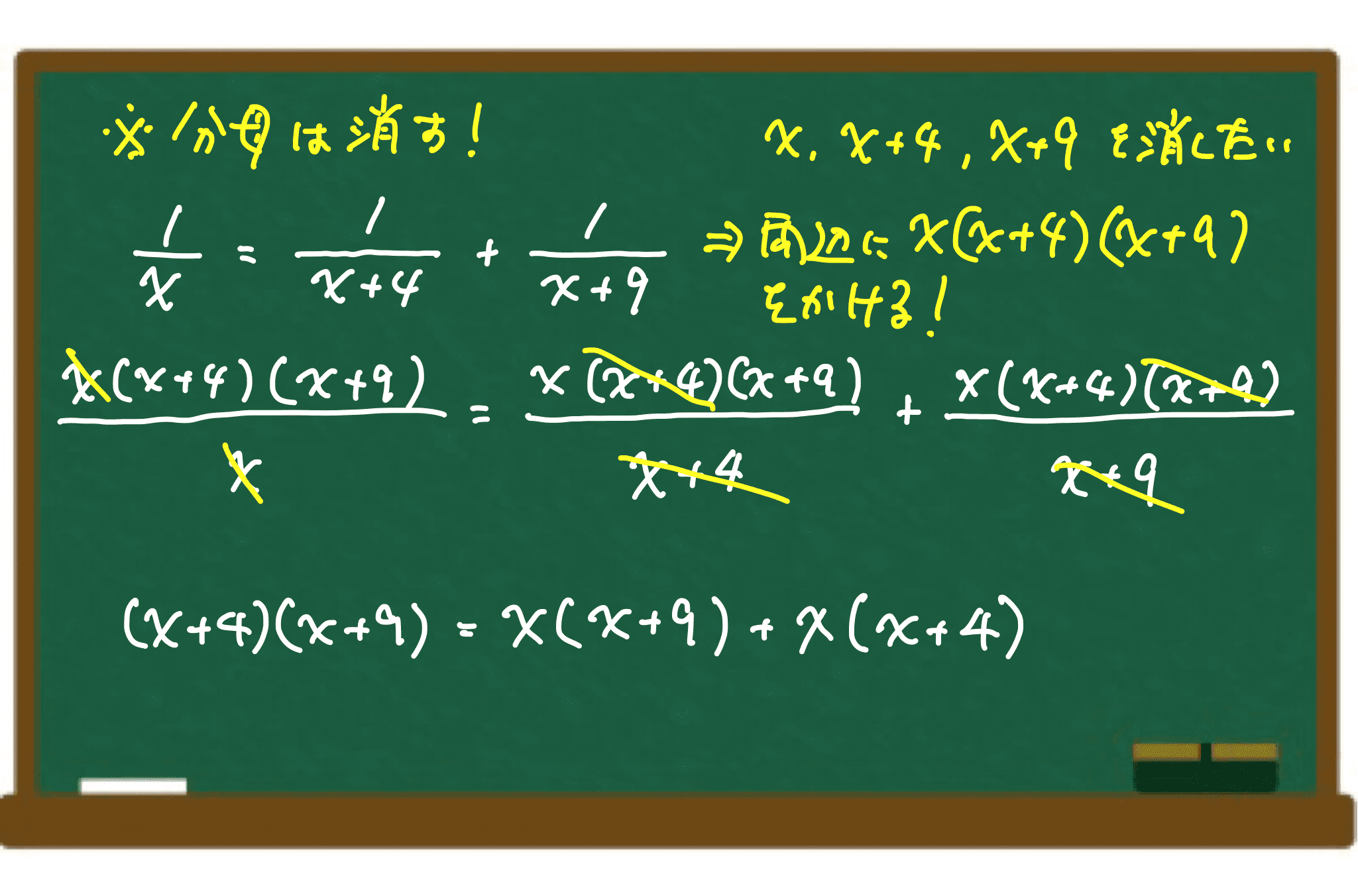



分数の計算 公務員試験のプロが独学受験生を応援するブログ




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題
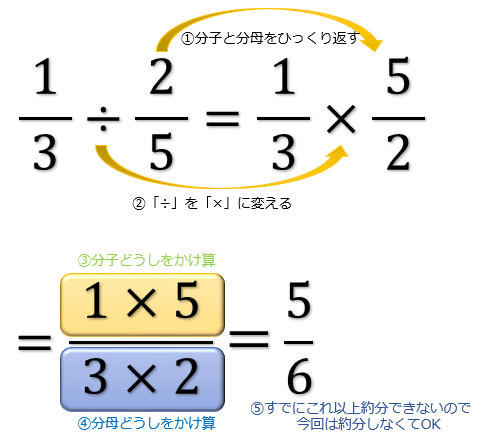



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




文字式の分数計算問題の4つのパターン Qikeru 学びを楽しくわかりやすく




連立方程式 分母の数が大きい場合の計算 中学生からの勉強質問 数学 進研ゼミ中学講座



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料
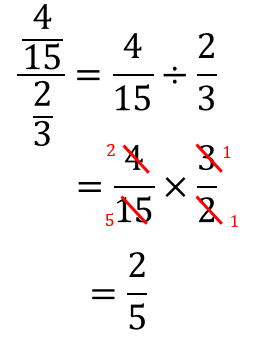



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




分数の足し算 帯分数どうし Youtube




帯分数の足し算 通分あり Youtube




分母ちがう分数の計算 分母足したらアカンよー 都立入試の情報満載 こじんまりしたこじま塾ブログ
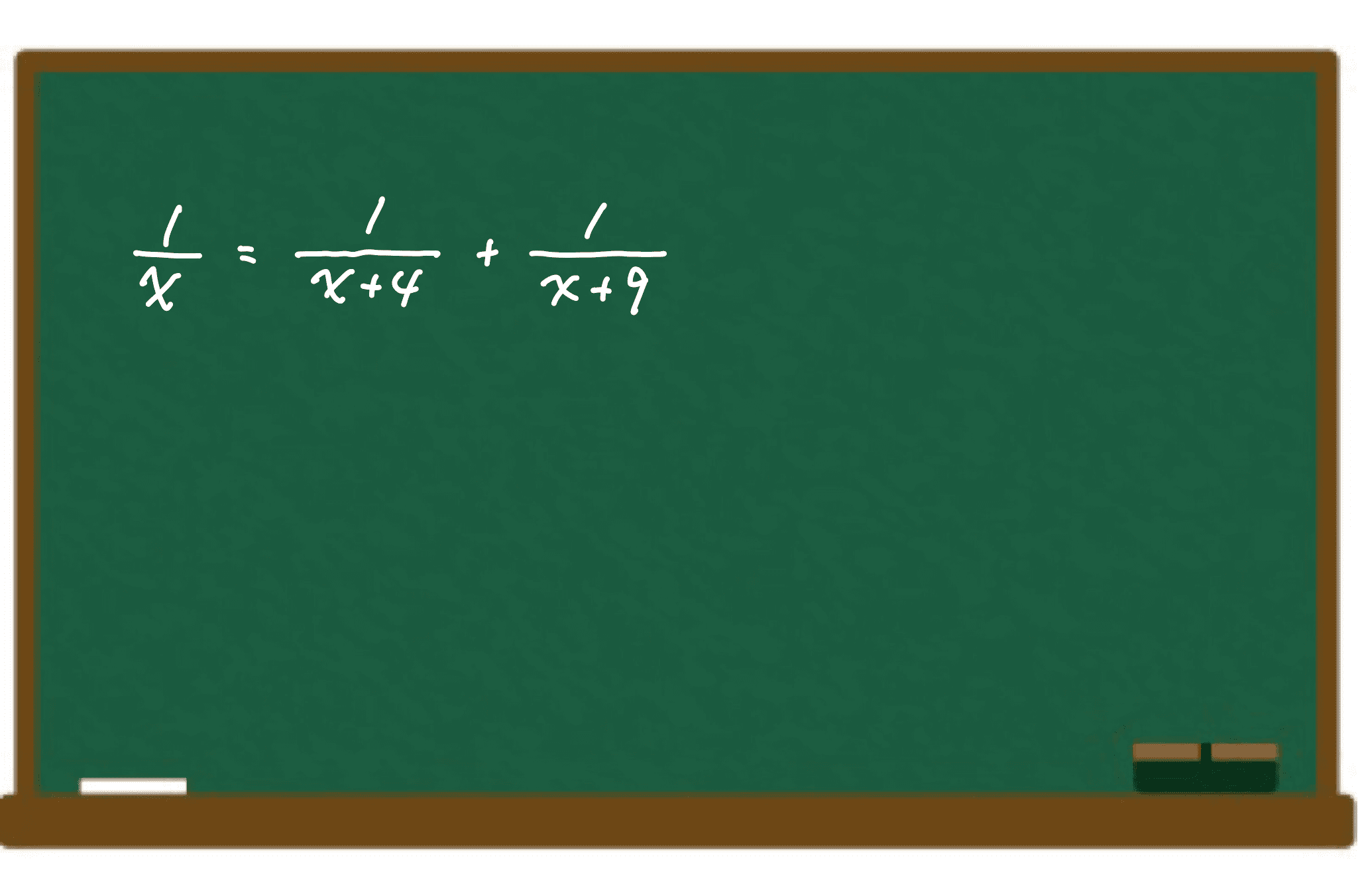



分数の計算 公務員試験のプロが独学受験生を応援するブログ




分数の引き算 分母が異なる 計算ドリル 問題集 数学fun




高校数学 繁分数式 分数の分数 の計算 受験の月
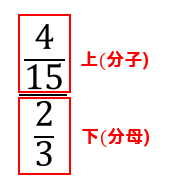



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
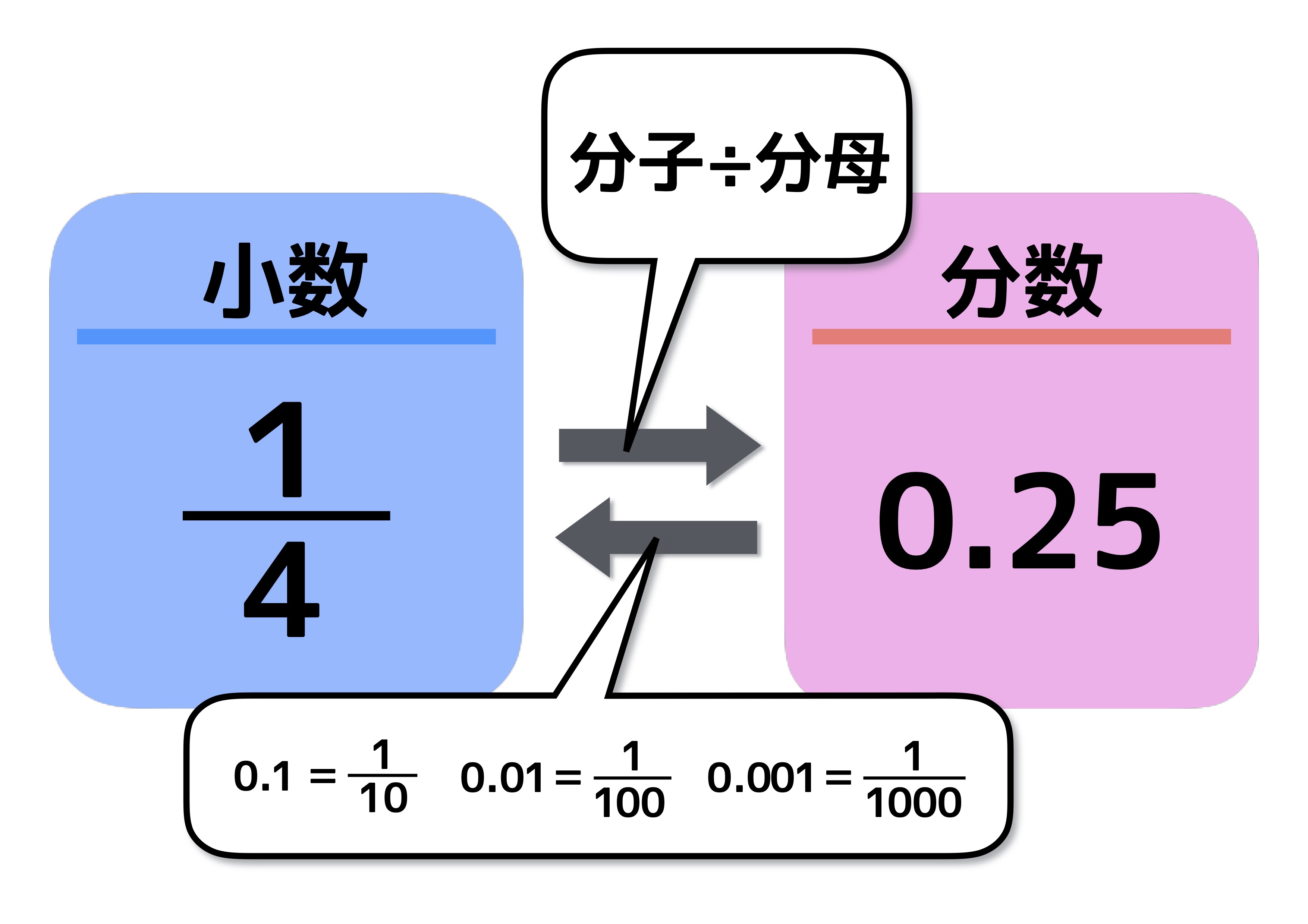



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ
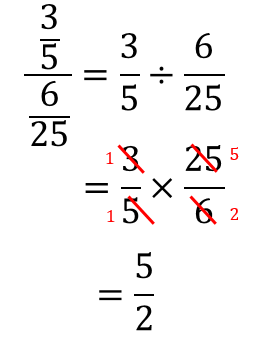



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
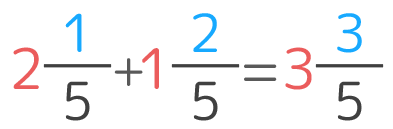



小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館
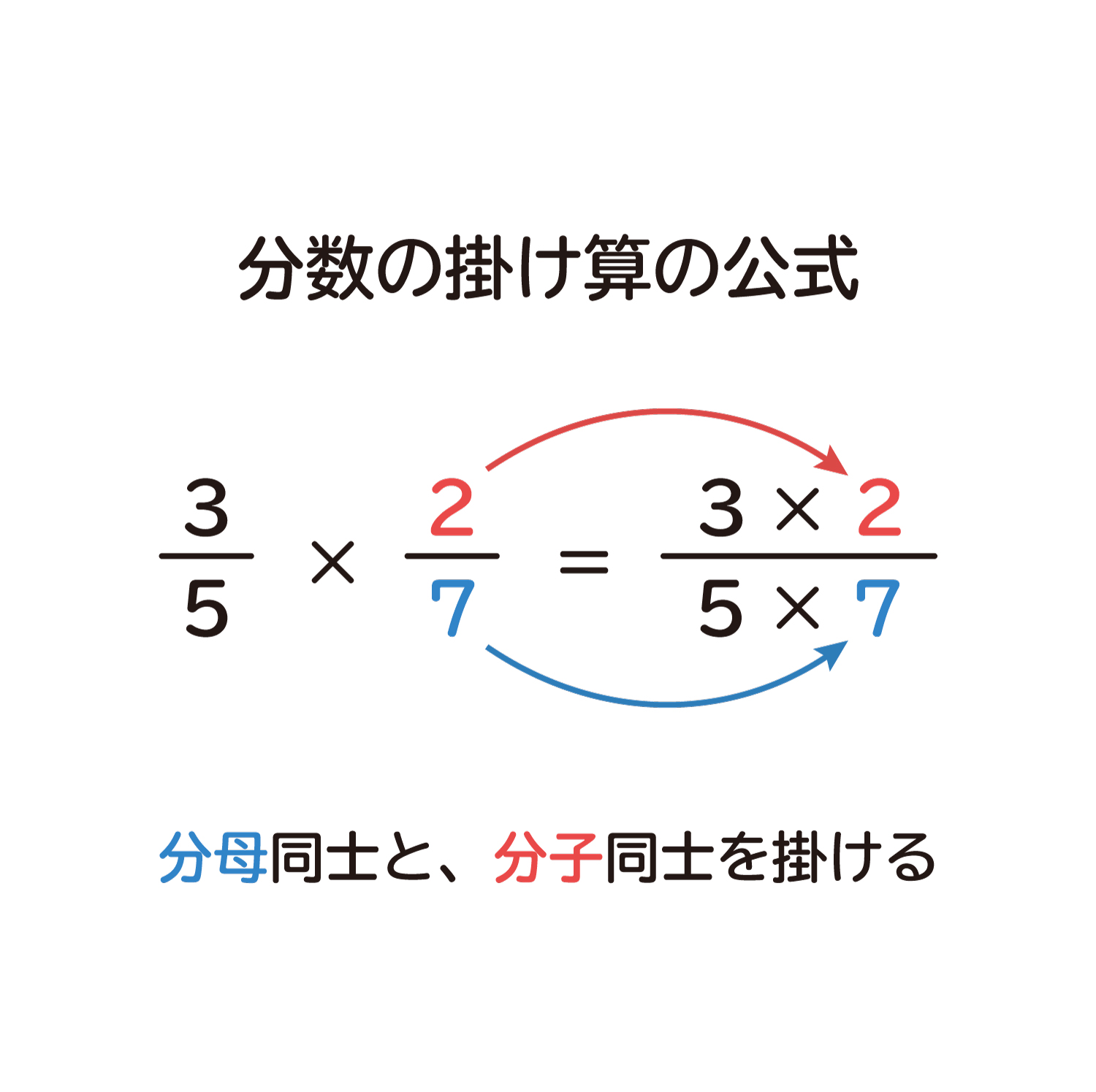



なぜ 分数の掛け算は分母同士 分子同士を掛ける のか を説明します おかわりドリル



分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋
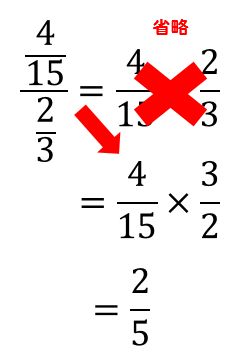



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ




小学校5年 算数 分数のひき算1 分母がちがうひき算 通分 Youtube
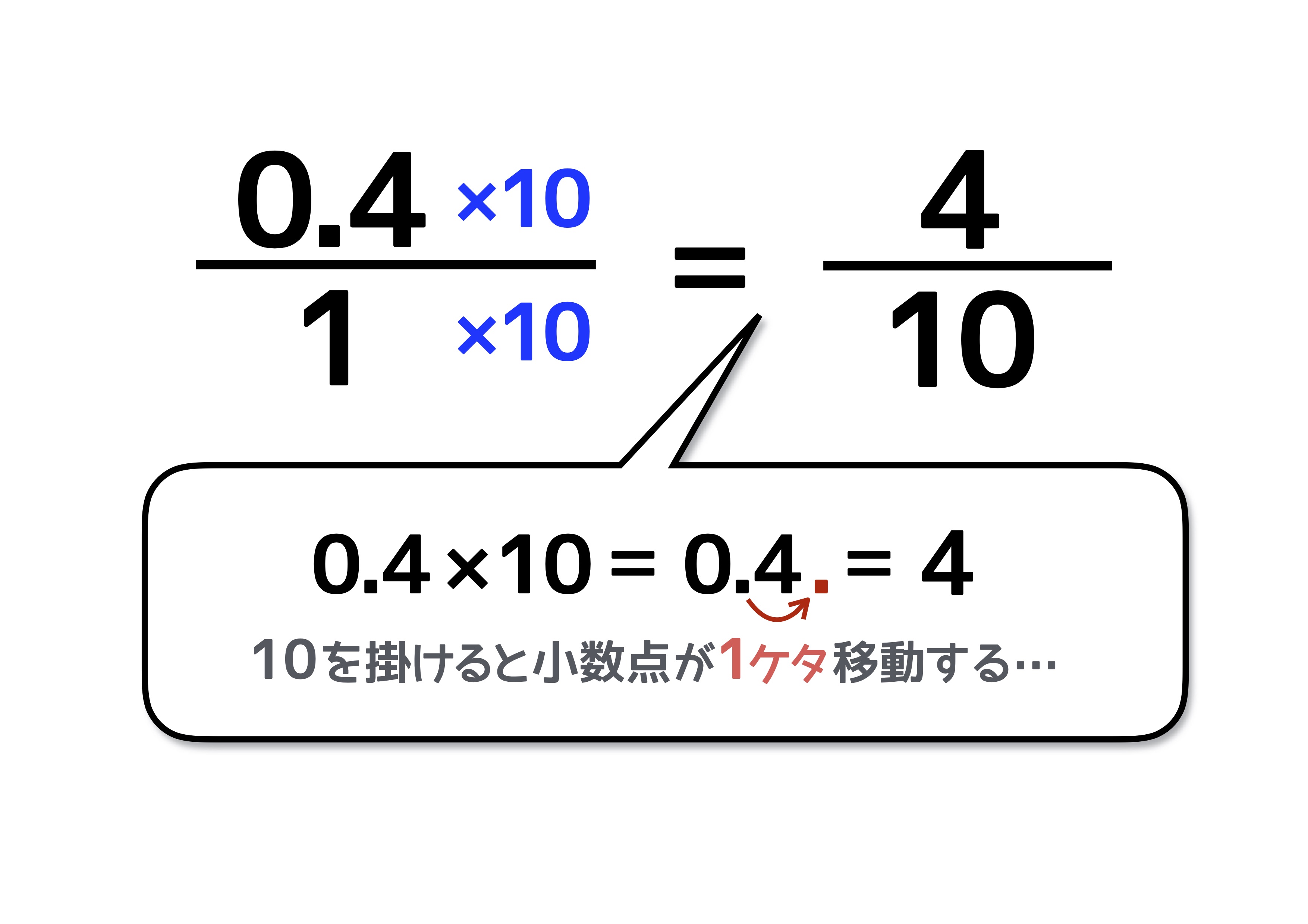



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




このような分数の計算でこの式の場合は通分していますが 分母同士で最小公倍数をかけて分 Clear
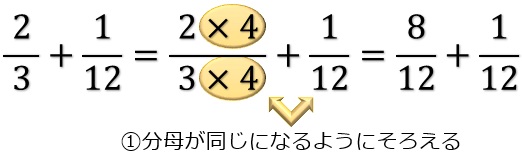



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ
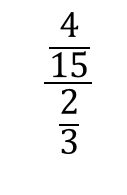



分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ




小学4年生の算数 同じ分母の分数のたし算 練習問題プリント ちびむすドリル 小学生




分数の掛け算は なぜ分母同士 分子同士を書けるの 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




文字が入った分数の足し算や引き算 分子にかっこをつけて通分する 中学や高校の数学の計算問題




分数の足し算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス
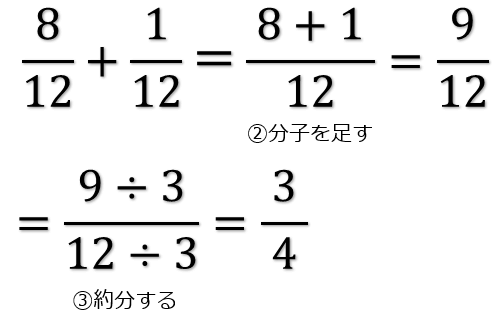



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ



異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料
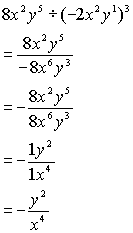



分数の復習と分数式の計算




分数の分数の計算方法 統計学が わかった




小学5年生の算数 異分母の分数の足し算 練習問題プリント ちびむすドリル 小学生




通分と約分 算数用語集



0 件のコメント:
コメントを投稿