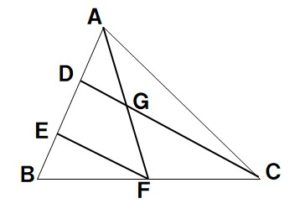
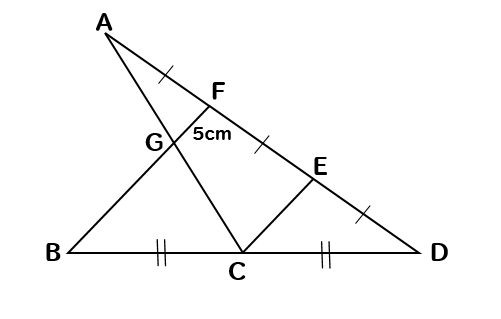
中点連結定理を根拠を明らかにして 証明することができる。 (思考・判断・表現)ワークシート ・気付いたことをノートにまとめるよ うに指示し,中点連結定理をまとめ る。 適用問題を解く。 本時の学習を振り返る。 6 練習問題を解く。 中点連結定理の演習問題問1 次の abcで、d,eは辺abを3等分する点、fは辺bcの中点である。ef=14cmのとき、次の問いに答えなさい。(1)dgの長さを求めなさい。(2)gcの長さを求めなさい。問2 次の abcで、d,eは辺abを中点連結定理 abcでab,acの中点をそれぞれm,nとすると 連立の計算問題 基礎から標準問題までの練習問題と、例題による解き方の説明
授業実践記録 数学 新しい 定理 とその活用 啓林館
中点連結定理 問題
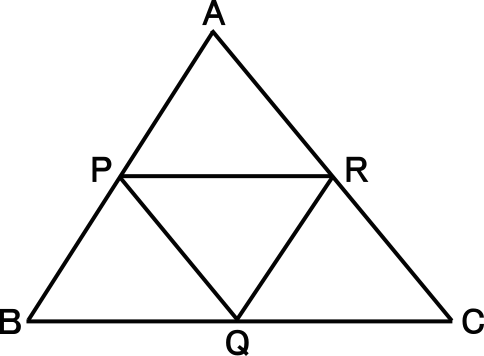
中点連結定理 問題-問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の定理の証明(2) 三平方これを「 中点連結定理 」といいます. 図1 AMN と ABC とは,相似比 12 の相似図形だから MNBC=12 になります. また, ∠AMN と ∠ABC とは等しいから, MN//BC になります. 問題1 右の ABC において, AB , BC , CA の中点をそれぞれ P , Q , R とし,辺の長



三角形 中点連結定理 入試正答率4 の問題 中学数学 理科 寺子屋塾の復習サイト
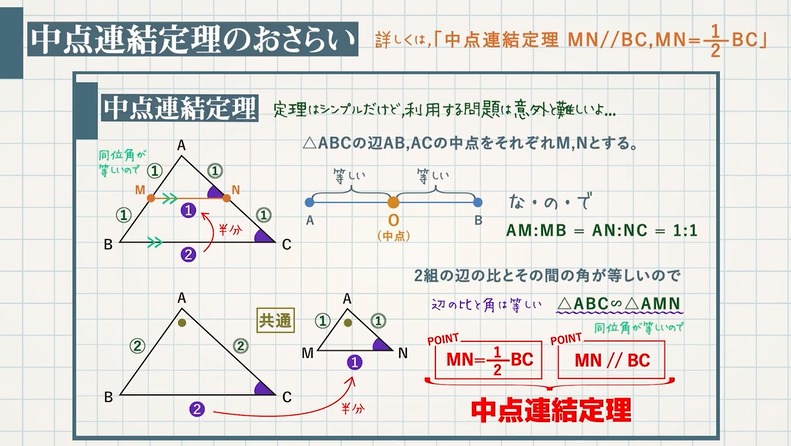
定理 三角形の底辺を除く2 辺のそれぞれの中点を結んだ線分「中点連結」は、底辺と平行であり、長さは底辺の半分に等しい。 証明 以下において、 ∥ は 2 つの線分が平行であることを表す。 三角形 abc について、辺 ab の中点を m, 辺 ac の中点を n とする。 このとき、三角形 abc の中点連結・ 中点連結定理が「線分の比と平行線」の特別な場合であると見ることができる。 ・ 中点連結定理を使って、証明を考えることができる。 段階 中点連結定理 は図形の問題で利用する機会の多い定理です。 この定理を利用することで 線分の長さ を求めたり、 平行であること を導くことができます。
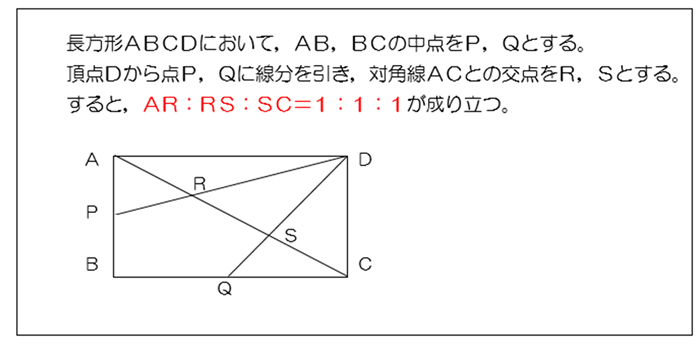
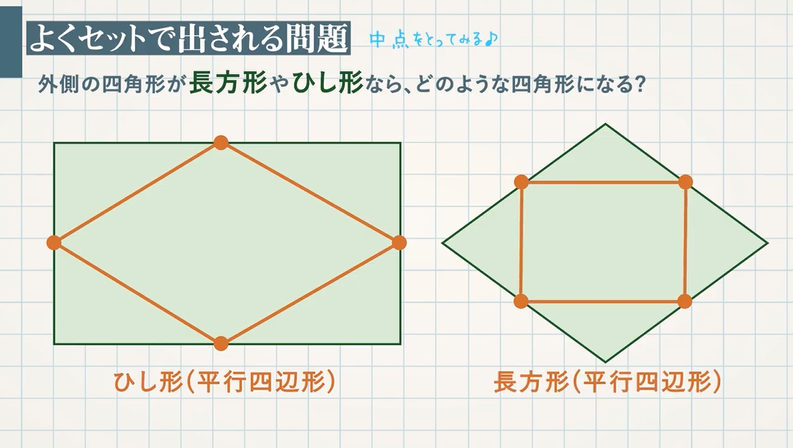
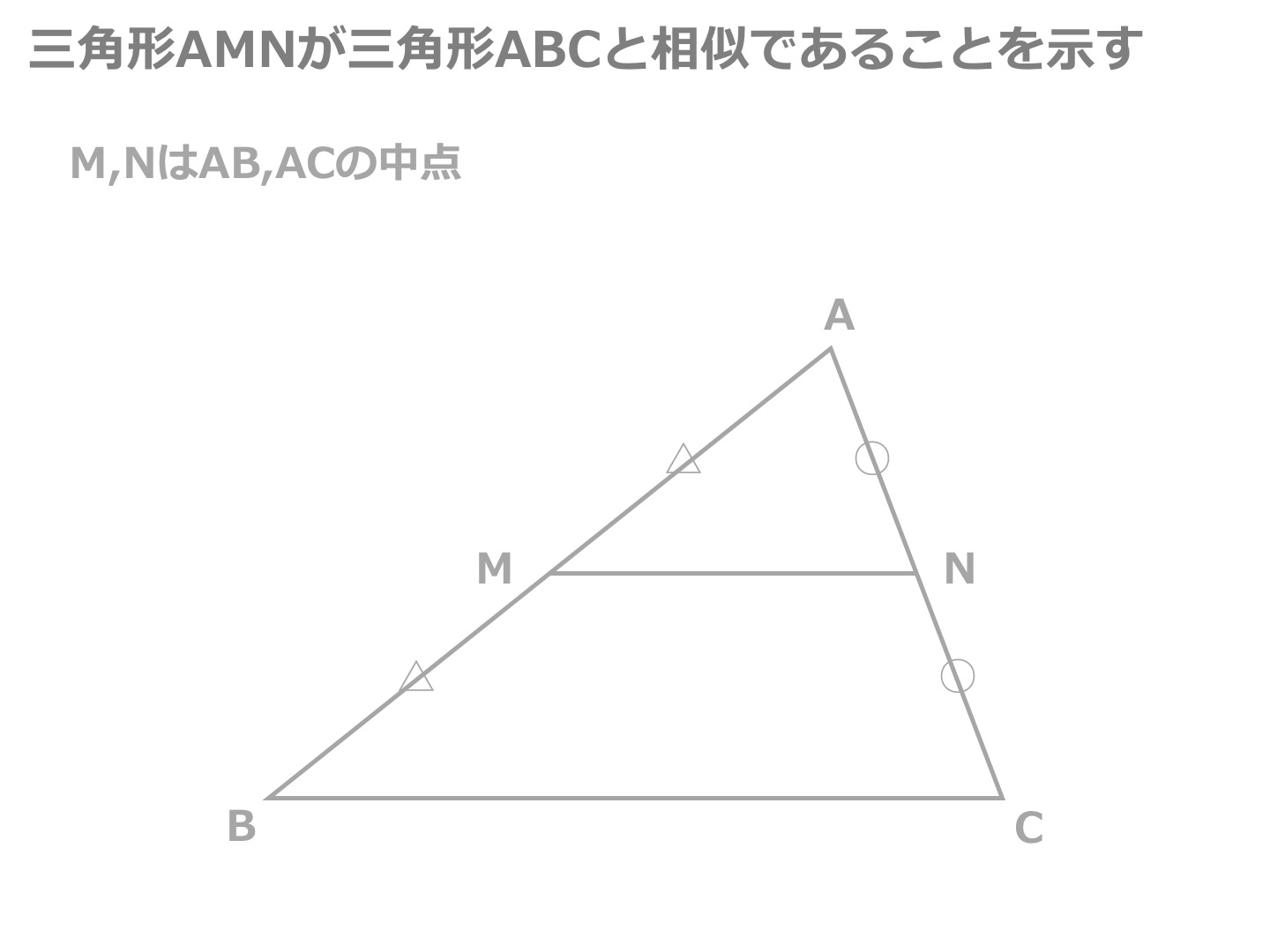
中点連結定理の証明がわかる3ステップ さっそく中点連結定理を証明していくよ。 3ステップで証明できちゃうんだ。 を思い浮かべてみて。 DとEはそれぞれ、ABとACの中点ね。 を証明することだよ。 さっそく証明していこう! Step1 相似の証明平面図形の基本的な定理である中点連結定理とその逆について紹介します. 中点連結定理とは 中点連結定理 とは,三角形の2辺の中点同士を結んだ線分に関する定理です.具体的には次のような主張です中点連結定理に関する問題や相似に関する問題で活用している先生や生徒がいるかもしれません。しかし,それをあえて"定理"としてまとめてみました。 (1)長方形を用いた場合 これが「 対角線3等分の定理
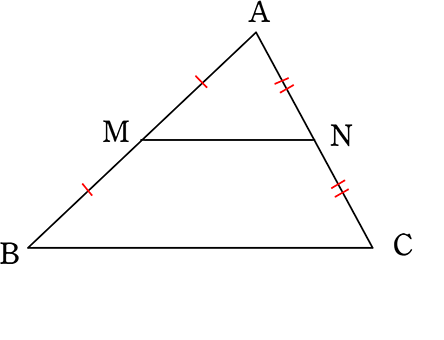
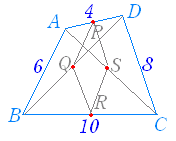
2 中点連結定理 問題集p18 茨abcの2辺ab,acの中点を, それぞれ,m,nとすると,線分mn と線分bcの間には,どんな関係があ るでしょうか。 上の abcで,am:ab=an:ac=1:2だから, mn⫽bc,mn:bc=1:2 が成り立ち,次の定理が得られる。 中点連結定理 定理四角形の4つの辺の中点を結んでできる四角形 はじめに この問題は,GCにとって,とても重要な問題である中点連結定理は、三角形の頂角をはさむ \(2\) 辺上にそれぞれ \(2\) つの中点をとるとき、『 中点を結ぶ直線と三角形の底辺は平行で、中点を結ぶ直線の長さは底辺の長さの半分になる 』というものです。



中3数学 中点連結定理の定期テスト対策問題 Examee




中3数学 中点連結定理を使う証明 練習編 映像授業のtry It トライイット
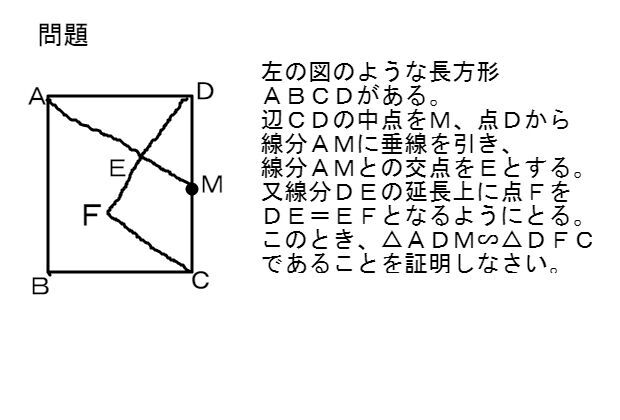
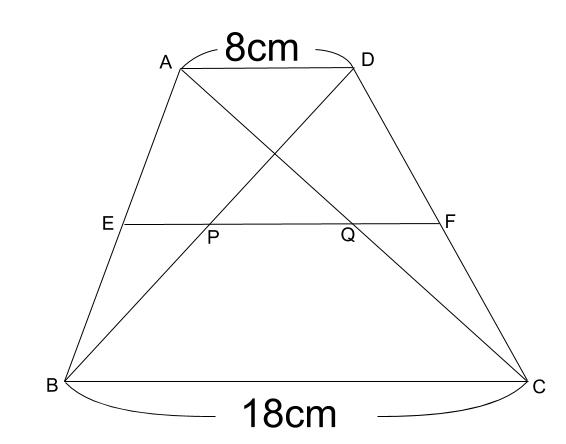
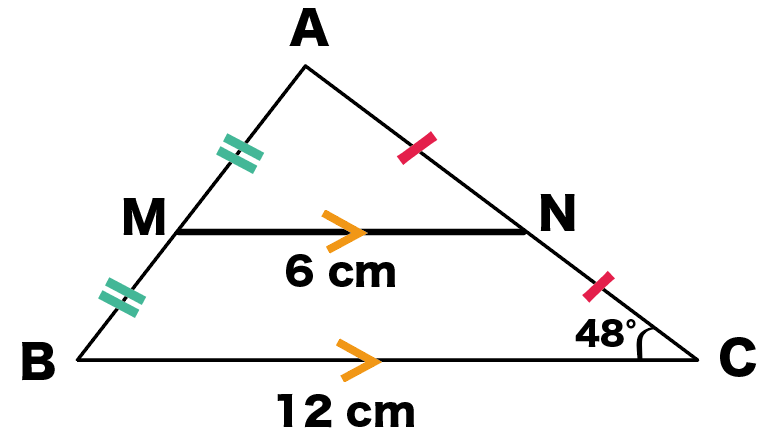
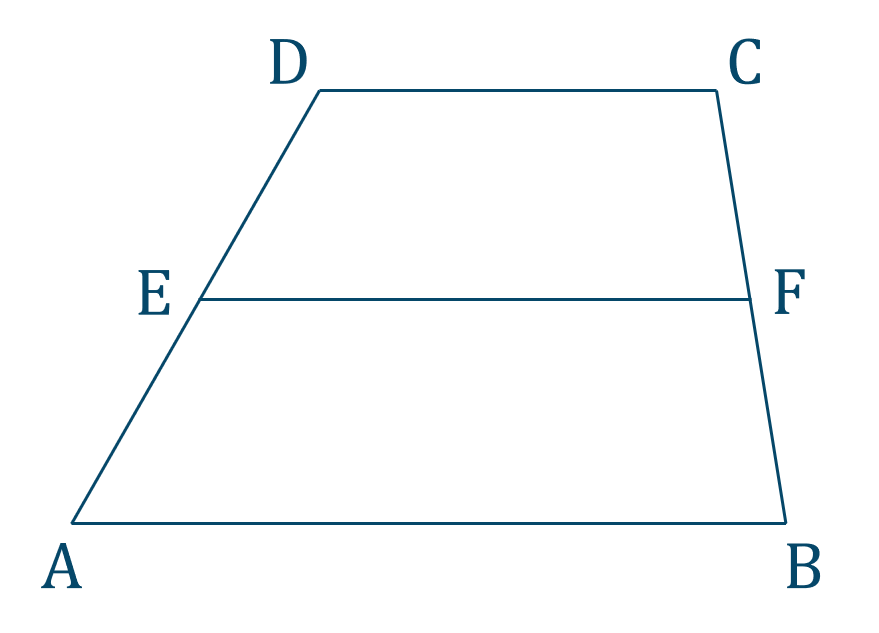
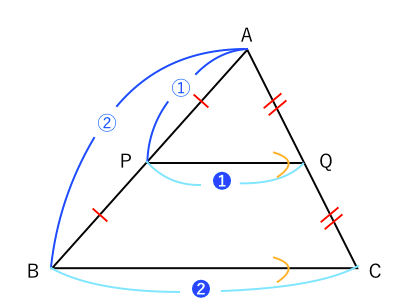
中点連結定理とは? 「中点連結定理」とは以下のように表現されます。 従ってそのは、それぞれの結論と仮定の一部を入れ替えて、• このとき、EFの長さを求めなさい。 問題に戻ると、上底のADの長さは6cm、下底のBCの長さは12cm、したがって、 となります。中点連結定理1 問題1 右の ABC において, AB , BC , CA の中点をそれぞれ P , Q , R とし,辺の長さをそれぞれ AB=8 , BC=10 , CA=6 とするとき,次の辺の長さを求めなさい. __________PQ= __________QR= __________RP= 採点する やり直す ヘルプ ABC において AB,BC の中点が三角形を三等分した問題の解説! 練習問題で理解を深める! 中点連結定理 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがで




中点連結定理の問題です の問題が分からないので 教えてください お願いします Clear
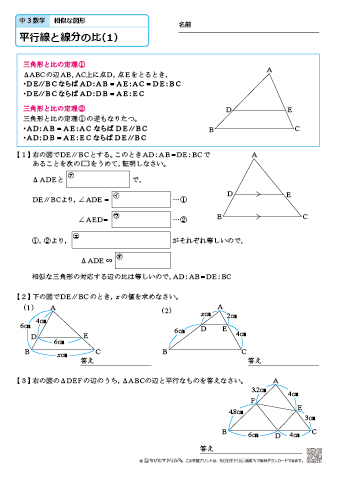



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
で,中 点連結定理が導き出され,中 点連結定理の理解が 促進されるような展開となるようにしていく。また,平 行線と線分の比の特別な場合が中点連結定理であること を認識させる。 第四次の相似比と面積比に関しては,中点連結定理で中点連結定理について詳しく解説!問題付き 中3数学で相似を勉強していると、 中点連結定理(ちゅうてんれんけつていり) を習うよね?? 中点連結定理とはその名前の通り、 line 始めました。中点連結定理1 中点連結定理 abcでab,acの中点をそれぞれm,nとすると mn//bc, mn= 1 2 bcとなる。 a b c m n ad//bcの台形abcdで、abの中点をe, dcの中点をfとする。




35 中点連結定理 三角形の重心 Youtube
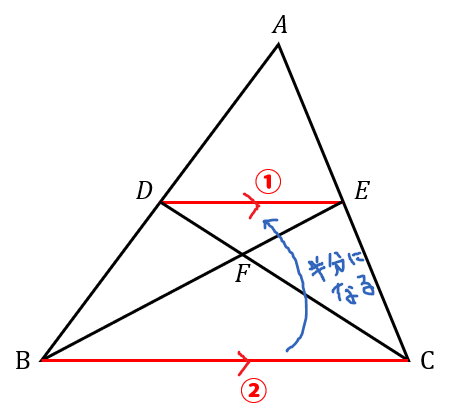



これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ
このページでは、中点連結定理について ・中点連結定理とは何か? ・中点連結定理の証明方法は? ・中点連結定理を使う問題はどうやって解くのか? といった疑問にお答えします。こんにちは、ウチダです。 今日は、中学3年生で習う 「中点連結定理」 について、まずはその証明を与え、次によく出る問題3つを解き、最後に中点連結定理の応用を考えます。 特に「中点連結定理と平行四辺形には深い結びつきがある」ことを押さえていただきたく思います。 中点連結定理、直角、二等辺三角形を利用した問題は、 5月の記事「少しずつ消化して」で紹介したように、 今春の大阪府公立入試一般選抜のb問題で出題されました。 「少しずつ消化して」の問題は円や三平方の定理が絡んでいて
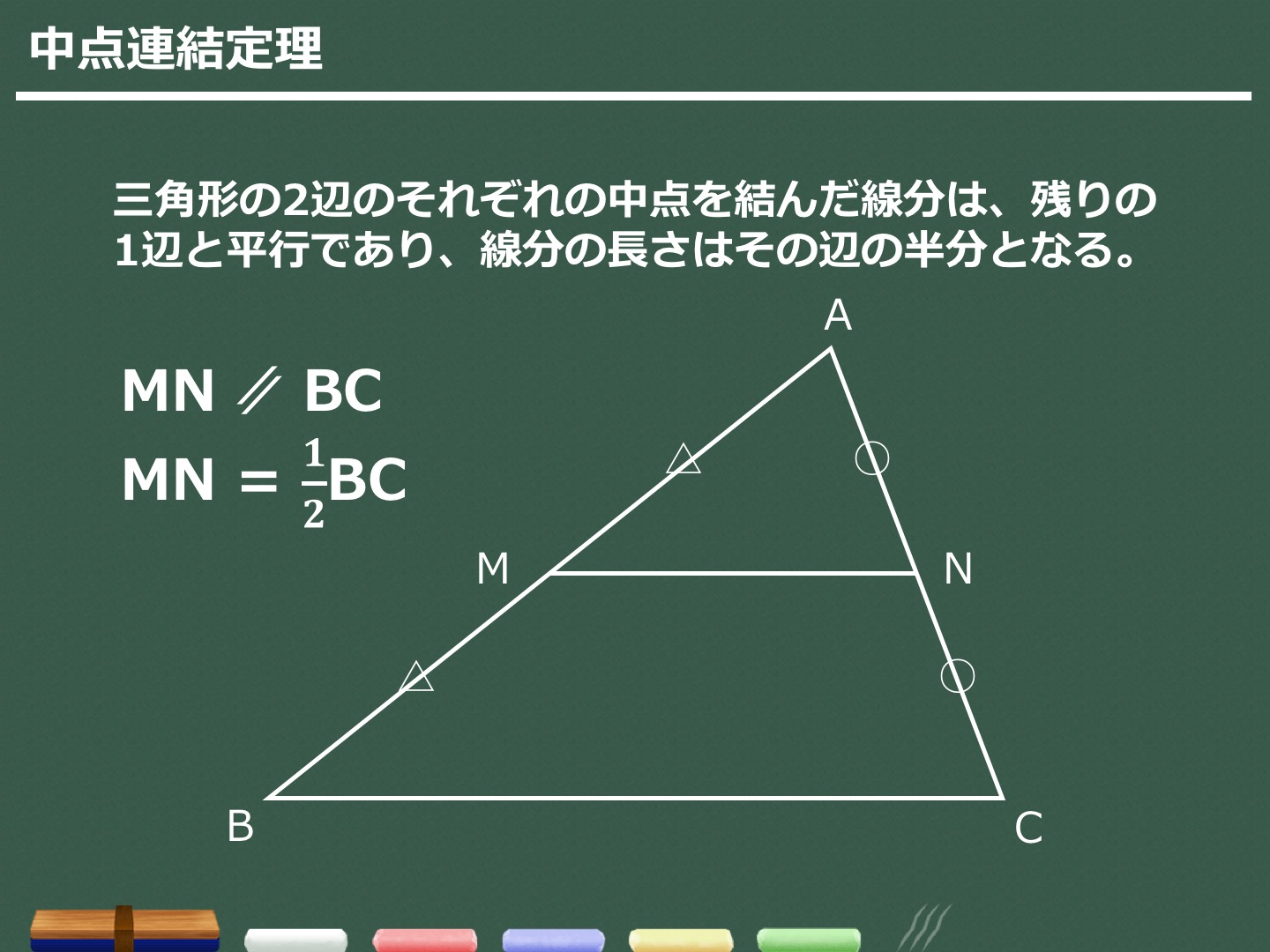



3分でわかる 中点連結定理の証明 問題の解き方をわかりやすく 合格サプリ



Studydoctor中点連結定理 中3数学 Studydoctor
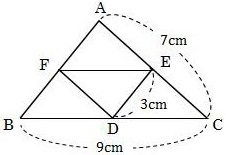
中点連結定理の演習問題問1 次の abcで、d,eは辺abを3等分する点、fは辺bcの中点である。ef=14cmのとき、次の問いに答えなさい この映像授業では「中3 数学 相似13 中点連結定理2」が約15分で学べます。 問題を解くポイントは「中点連結定理は、① 底辺がち,中点連結定理について調べようと 行線と線分の比についての関係を,意 する。 欲的に調べようとしている。 見方や考え方 中点連結定理の証明を,根拠を明らか 自力解決で,自分なりに証明をし, にしながら,証明することができる。中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!台形の面積比問題を解説! 円錐の体積比を解説!




数学 中 点 連結 定理




中3数学 中点連結定理を使う証明 例題編 映像授業のtry It トライイット
, ← , , 中点連結定理 / 定理の内容( GC World 2 いろいろな問題 ,有名な定理 ) 三角形の2辺 AB,AC の中点をそれぞれ D,E とするとき, DE // BC「エレガントな問題を作る。」にもありますが、私が この問題をはじめて見たのは「青チャート・数学A」 でした。もちろんワカリマセンでした。「中点連結 定理」の使い方は面白いと思います。中点連結定理 abc で,2 辺ab,ac の中点を,それぞれ,m,n とすると mn // bc ,mn =bc がいえる。これを中点連結定理という。 これは,特に新しい内容ではありません。「5線分の比と平行線」で比が




中点連結定理を使った図形問題 9il3lcfxqzegolq Twitter



お礼500枚中点連結定理 の応用問題問題と解答を示します 解 Yahoo 知恵袋
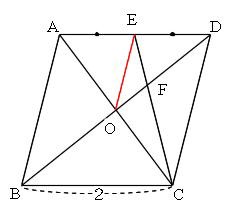
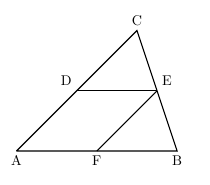
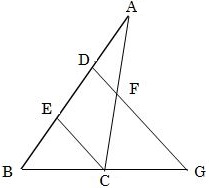
相似な図形 中点連結定理2 右の abcで、辺abの中点をm,辺bcを三等分 a する点をd,eとし、aeとcmの交点をfとする。



トッポの受験数学 特訓教室 図形 関数 図形の計量 問題6 解答 問題へ戻る ポイントと解説 正4角すい この問題では すべての辺の長さが等しいね その場合断面図は直角2等辺3角形 になることも暗記しておくべし ねじれの位置にある
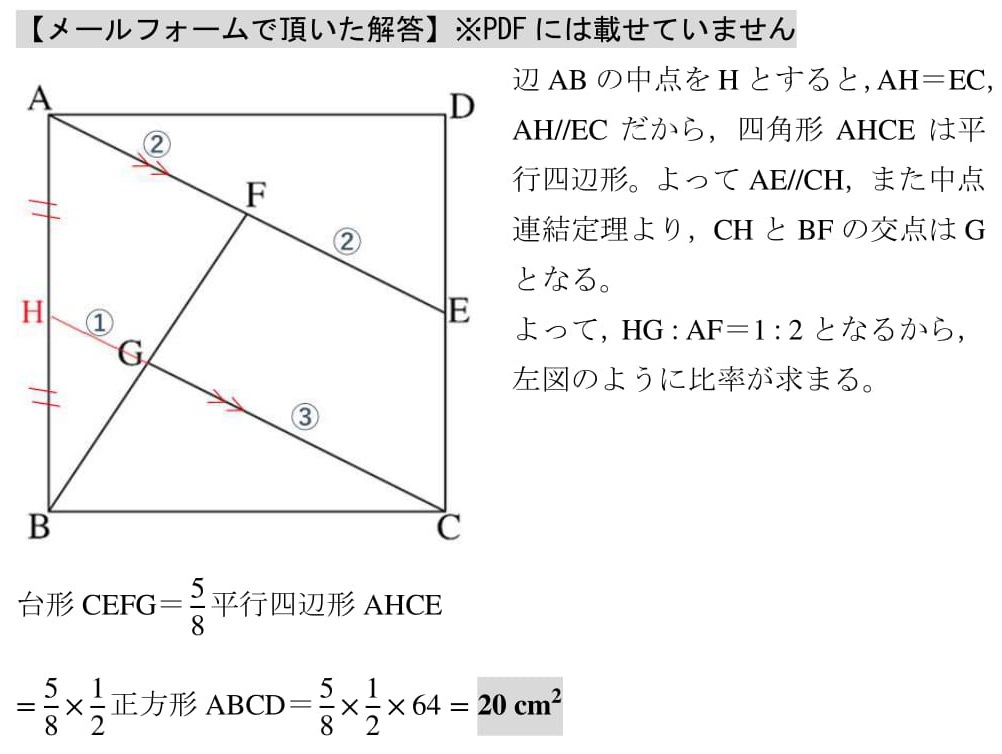



中点中点と裏技 21愛知県b 高校入試 数学 良問 難問




中3数学 中点連結定理を使う証明 例題編 映像授業のtry It トライイット




中点連結定理 きっずゼミ子育て応援ブログ



Q Tbn And9gcrg8zmq7bd51hnrsnn0g9gzfb1tpt09kazrxxddw A6niifuh Usqp Cau




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear
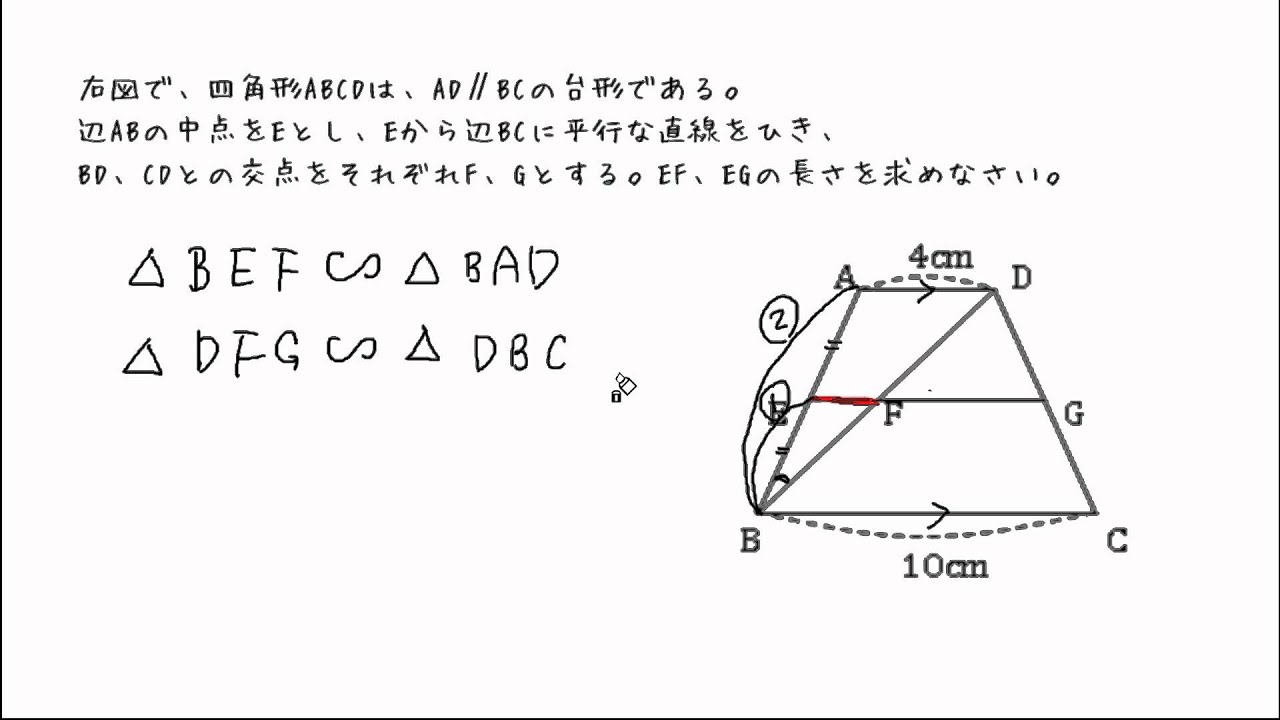



中点連結定理 問題 Youtube




中学3年の数学 動画 平行線と線分の比 中点連結定理編の問題 19ch




中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
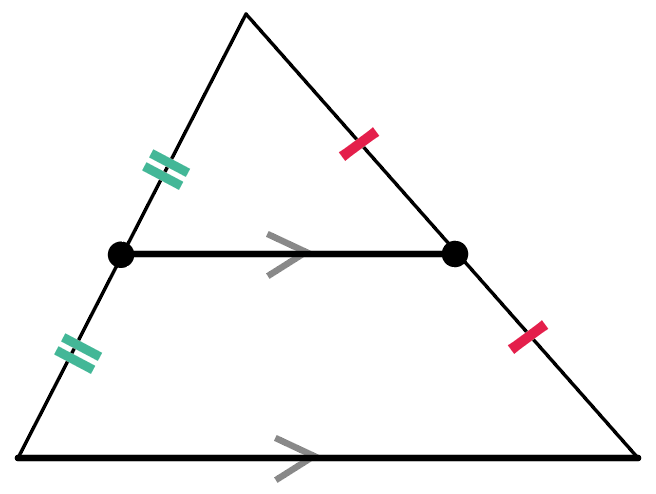



中3数学 2分でわかる 中点連結定理とは Qikeru 学びを楽しくわかりやすく



第178回 数学 三角形をさがせ 解答 解説 家庭教師が伝授する具体的な成績アップの勉強法と秘訣を公開



中2の数学の問題で わからないところを教えてください 出題範囲三角形と四角 Yahoo 知恵袋
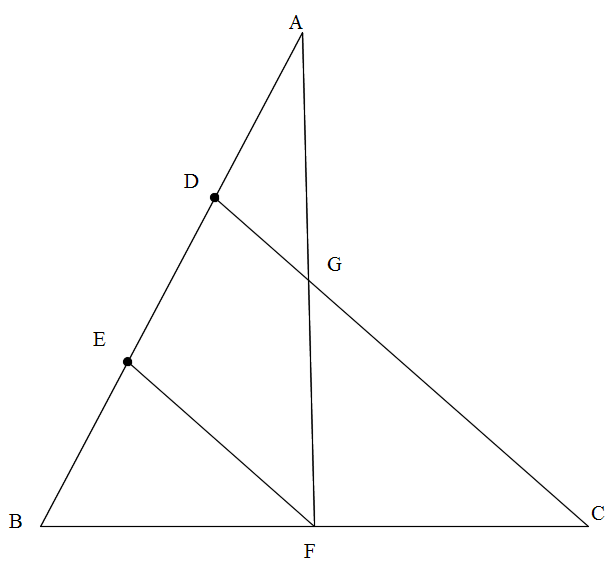



中点連結定理 中学入試 高校入試 算数 数学質問所




中点連結定理とは 証明 問題の解き方の解説 数学fun



中点連結定理 思考力を鍛える数学




中点連結定理を使った証明 Youtube
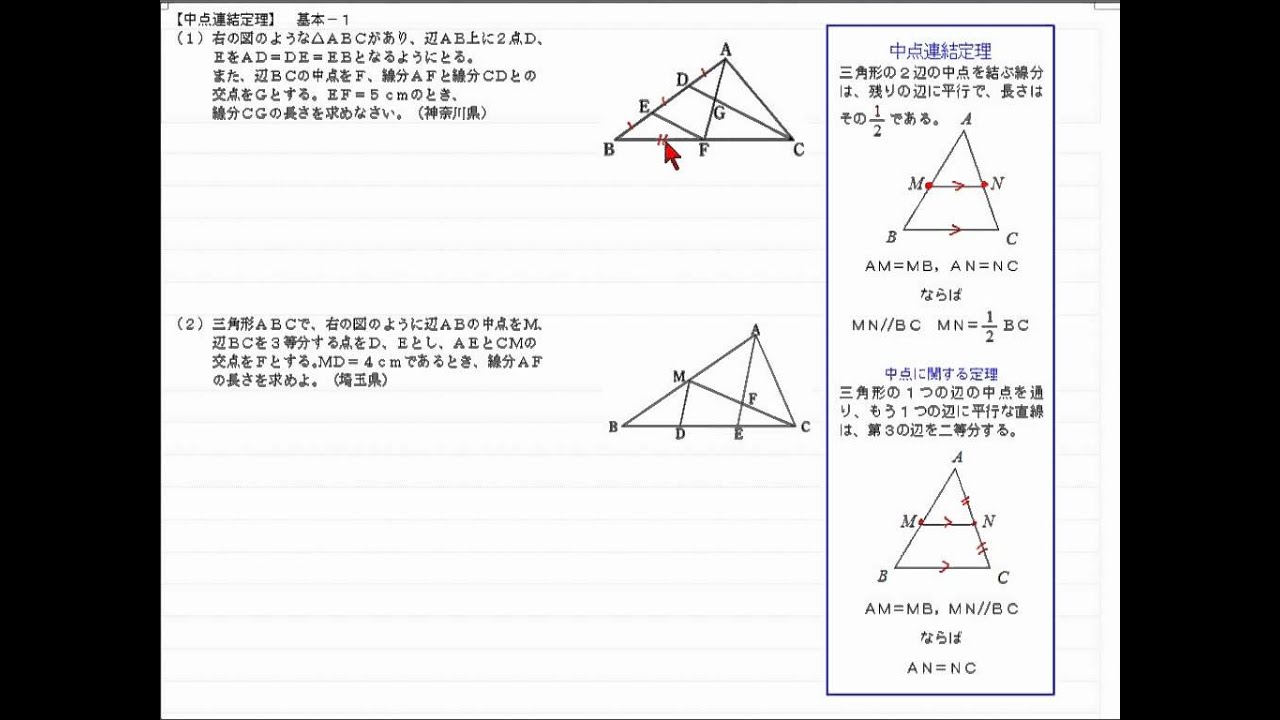



No 393 中3数 相似な図形 中点連結定理 基本1 ネット塾の英進塾 Youtube
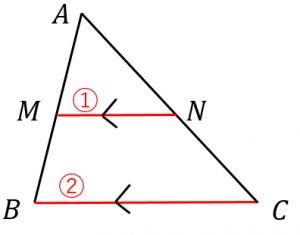



中点連結定理とその逆の証明および例題 具体例で学ぶ数学
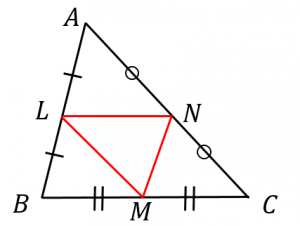



中点連結定理とその逆の証明および例題 具体例で学ぶ数学
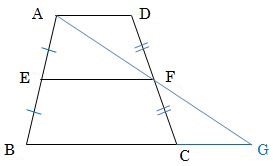



中3数学 中点連結定理ってどんな定理 まなビタミン




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学
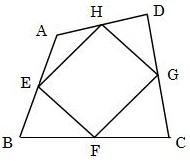



中3数学 中点連結定理ってどんな定理 まなビタミン



図形問題が驚くほど得意になる基本問題とは あおぞら塾




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor中点連結定理の利用 中3数学 Studydoctor
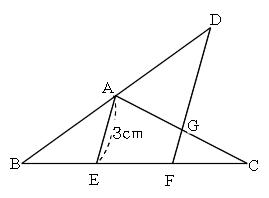



Mathematics 相似 5 中点連結定理と重心 働きアリ



中点連結定理
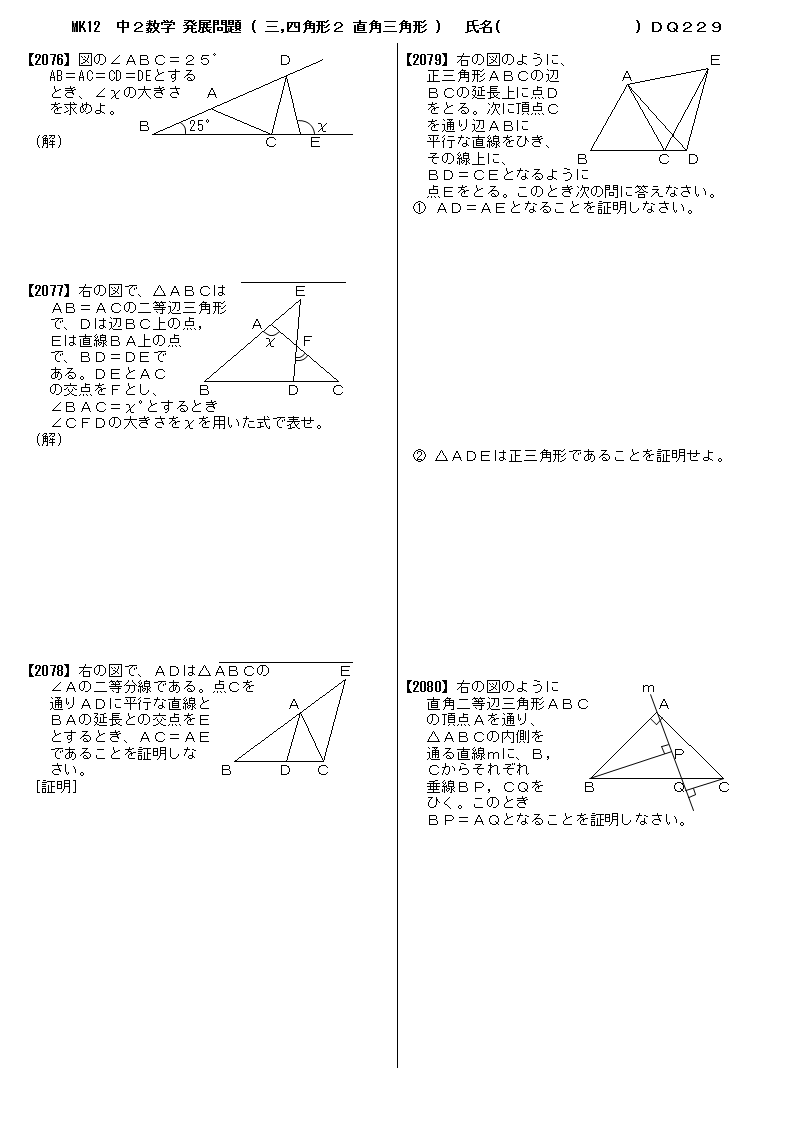



無料 中2数学 応用 発展問題 問題プリント 329 図形の相似4 中点連結定理



Studydoctor台形と中点連結定理 中3数学 Studydoctor




授業実践記録 数学 新しい 定理 とその活用 啓林館



Http Www Nyushi Sugaku Com Tyu3 T3 5 Y 06 Pdf



第5章12 中点連結定理 中点連結定理 フロントエンドなブログ
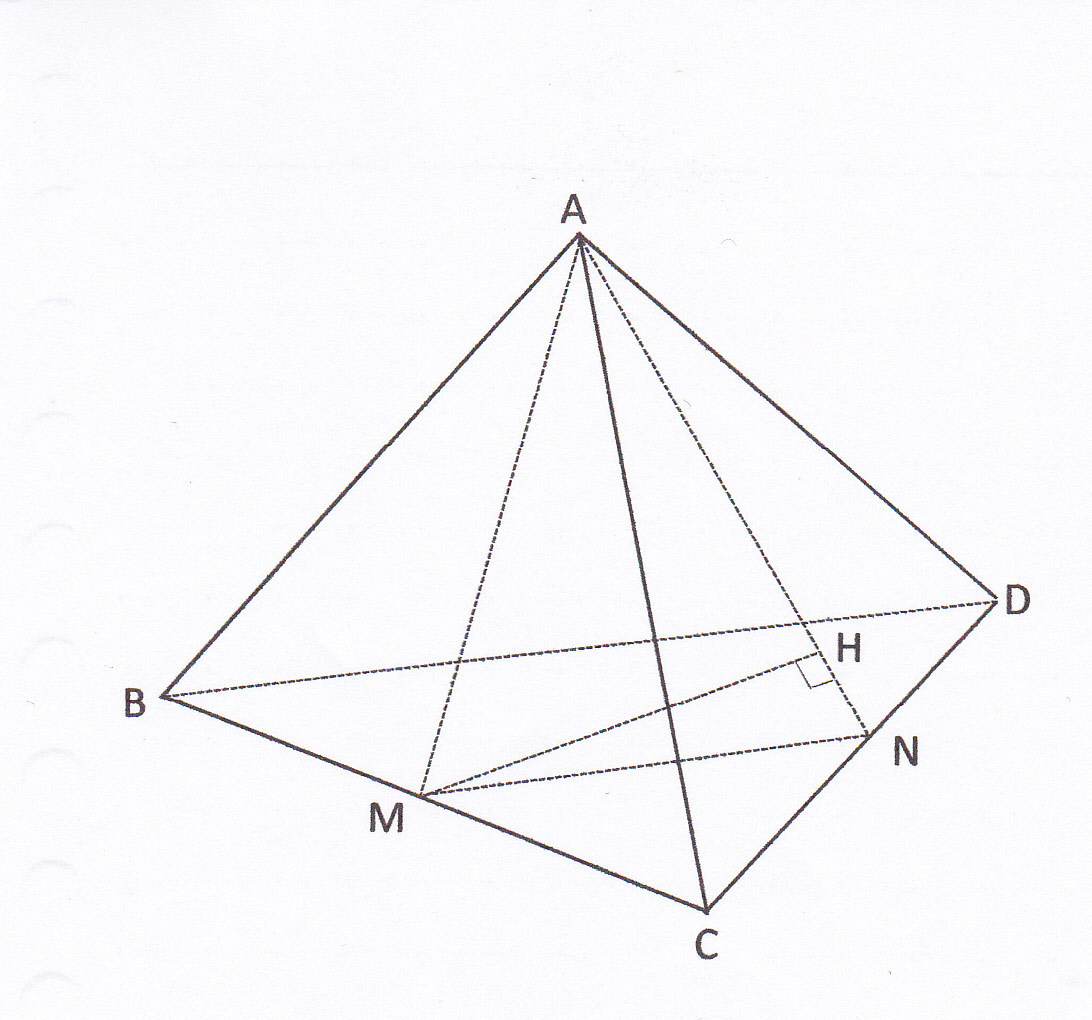



三平方の定理 中点連結定理と空間図形の融合問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中点連結定理とは 三角形の問題で使い方をマスターしよう 中学や高校の数学の計算問題
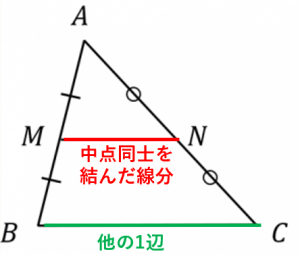



中点連結定理とその逆の証明および例題 具体例で学ぶ数学



1



中3相似 中点連結定理 三等分の三角形求め方を問題解説 数スタ
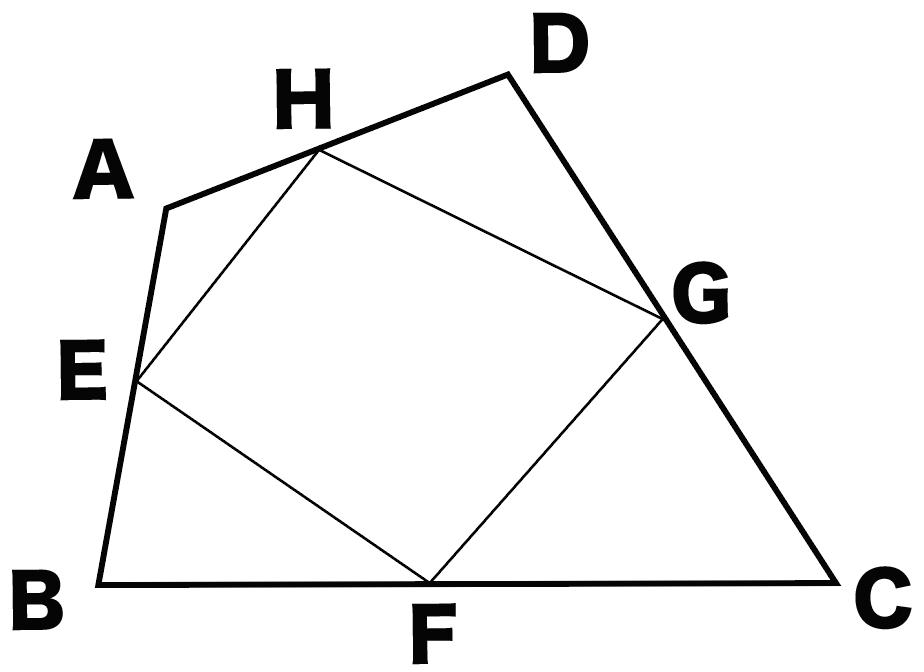



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




数学も英語も強くなる 意外な数学英語 Unexpected Math English April 16




世界一わかりやすい数学問題集中3 5章 図形と相似




中学数学 正答率2 1 公立高校入試で出た平面図形の難問 定期テストや高校入試に レオンの中学数学探検所



Http Mathaca Com Download 2 12kaisetu Pdf




中点連結定理の一証明 身勝手な主張




無料 中3数学 標準問題 解答プリント 329 図形の相似4 中点連結定理



第5章13 中点連結定理 中点連結定理と長さ 中学生




無料 中3数学 発展 応用問題 解答プリント 329 図形の相似4 中点連結定理



中学数学 中点連結定理 中学数学の無料オンライン学習サイトchu Su



Mathematics 相似 5 中点連結定理と重心 働きアリ
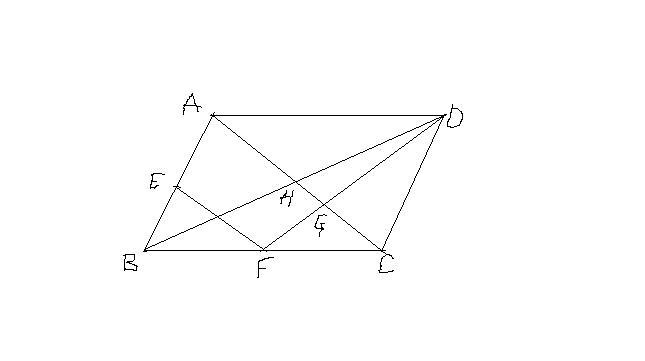



平行四辺形を題材にした平面幾何の問題です F1 数学 箱根駅伝ブログ




中点連結定理 チーム エン




三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア



中点連結定理 問題 On Vimeo



教材研究 中点連結定理



中点連結定理 問題 On Vimeo




中点連結定理 高校入試問題 数学 を毎日解いてみよう




至急です 三角形を中点連結定理とs Alを使って証明する問題です Clear
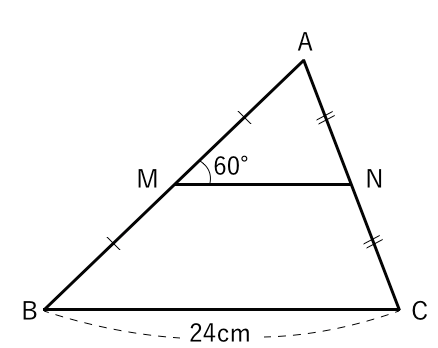



相似な図形 中点連結定理を使う 苦手な数学を簡単に



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典




中点連結定理 Abcの辺bc Ca Abの中点をそれぞれd E Fとす Okwave
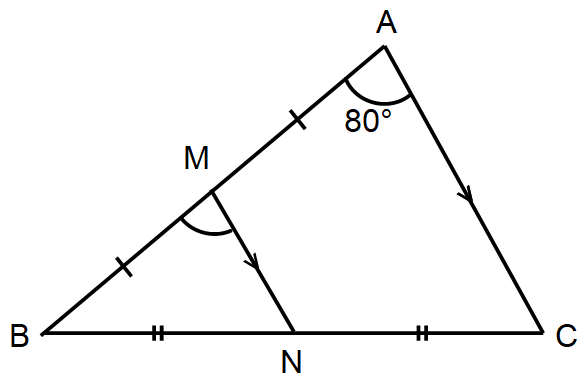



令和2年度 長野県立高校入試 大問1 11 ネット塾




三角形 中点連結定理 入試正答率4 の問題 中学数学 理科 寺子屋塾の復習サイト



中点連結定理を使った平行四辺形であることの証明 教遊者



台形と中点連結定理について 下の図においてどのようにしたら mn Yahoo 知恵袋



中点連結定理を使った平行四辺形であることの証明 教遊者



中学3年数学練習問題 中点連結定理 図形と相似



中3数学 2分でわかる 中点連結定理とは Qikeru 学びを楽しくわかりやすく




数学 中3 51 平行線と線分の比 中点連結定理編 Youtube




中点連結定理 無料で使える中学学習プリント



中点連結定理の問題の解法 夢を叶える塾



3分でわかる 中点連結定理の証明 問題の解き方をわかりやすく 合格サプリ
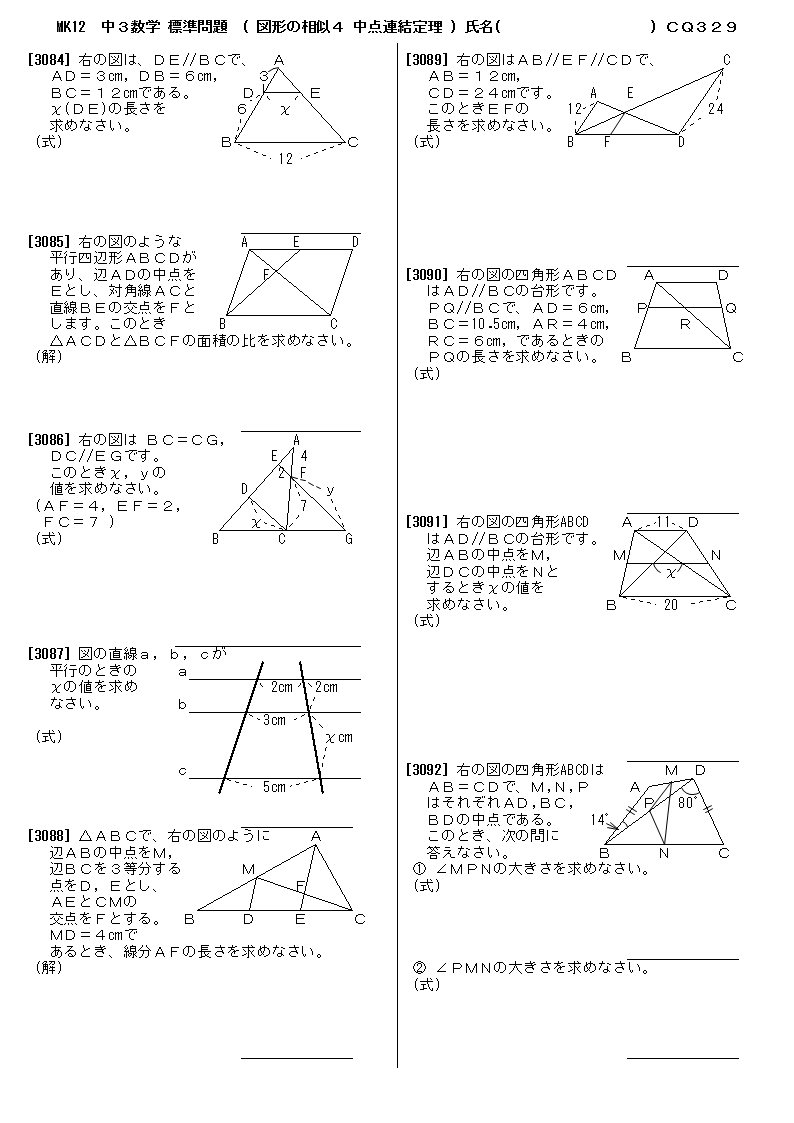



無料 中3数学 標準問題 問題プリント 329 図形の相似4 中点連結定理




中点連結定理を利用した証明 チーム エン




中3数学 相似 中点連結定理 Youtube



Mathematics 相似 5 中点連結定理と重心 働きアリ The 2nd



1



中点連結定理
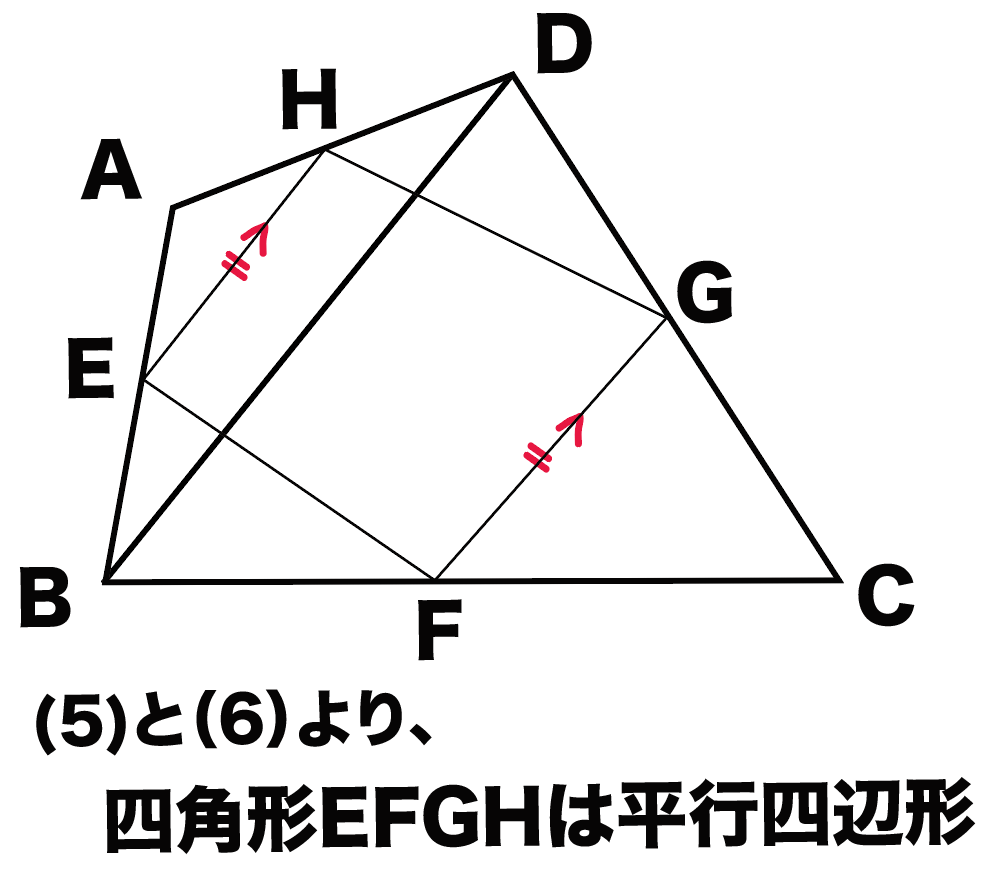



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中3 5章 図形と相似



数学a 中点連結定理と平行線と比の使い方とコツ 教科書より詳しい高校数学



中学数学 図形の相似



中点連結定理1



中3数学 中点連結定理ってどんな定理 まなビタミン



中3数学 中点連結定理ってどんな定理 まなビタミン




初等幾何学から4 中点連結定理 身勝手な主張



中2幾何です 中点連結定理の逆を使用する問題なのですが中点連結定理 Yahoo 知恵袋



中点連結定理とは 苦手な数学を簡単に




台形と中点連結定理 Ad の台形の辺abと辺cdの中点をe Fとす Okwave




中学数学の中点連結定理を使う初等幾何学の問題を1問解こう 身勝手な主張




至急です 三角形を中点連結定理とs Alを使って証明する問題です Clear



1
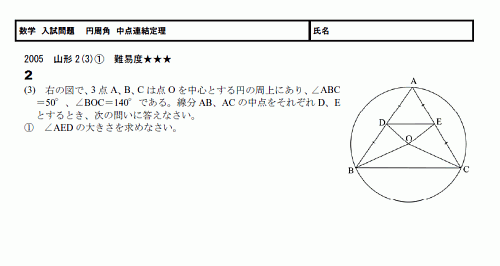



円周角 中点連結定理 スタディーx



0 件のコメント:
コメントを投稿